티스토리 뷰

NAVION 수직 꼬리 날개 분석
저번 글에서는 NAVION의 수평 꼬리날개를 주익과 같은 방식으로
분석하였습니다. 이번 글에서는 수직 꼬리날개를 분석하겠습니다.
수직 꼬리날개의 특징점은 양력이라는 말을 횡력이라는 말로
바꾸어 사용한다는 것입니다.
이 때문에 저도 좀 헷갈립니다.
하지만 이 또한 주익과 계산방식은 똑같습니다.
다만 양력이 횡력(Sideforce)으로 바뀐다는 점만 빼고 말입니다.

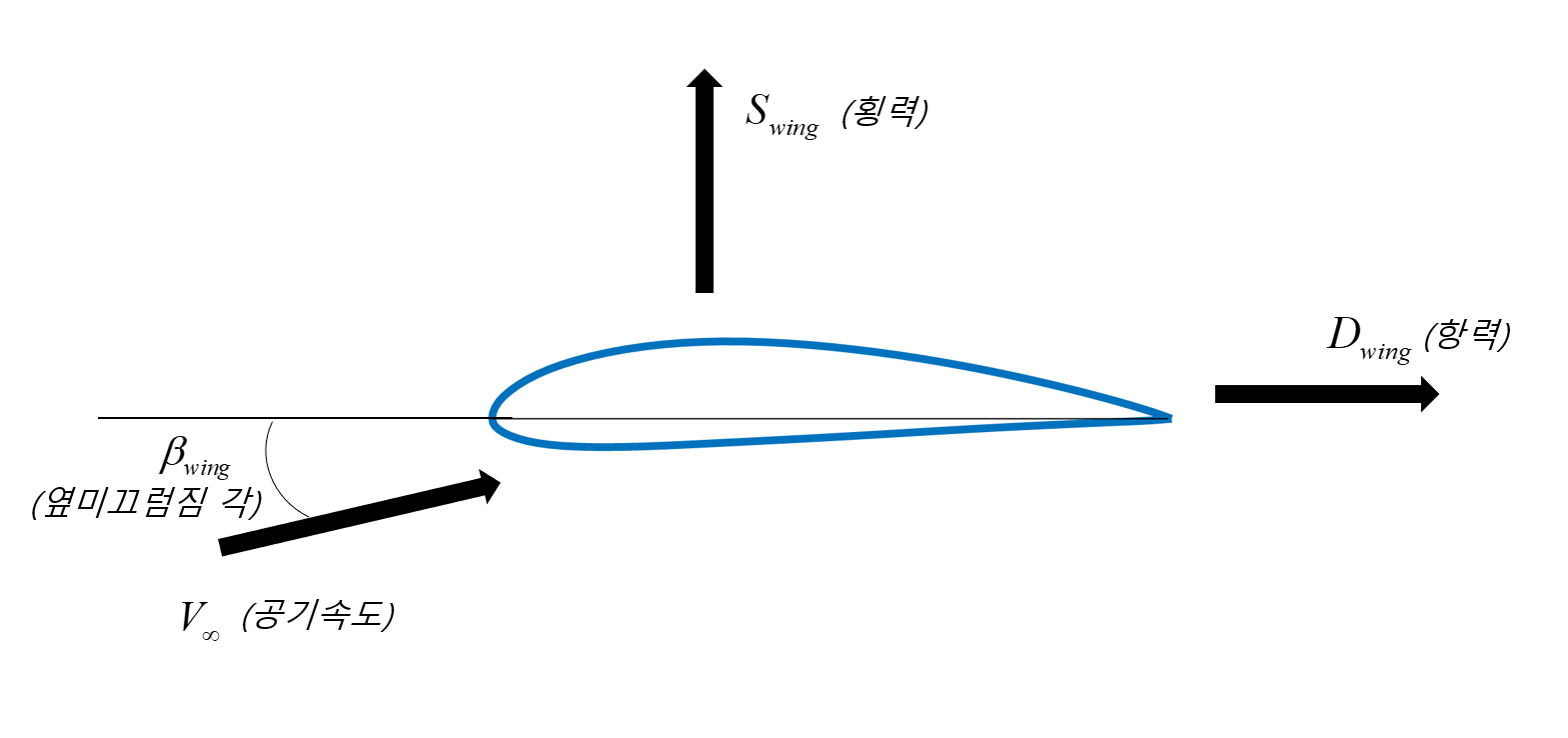
그림 27과 28을 보시면 감이 오실 겁니다.
양력이 횡력으로, 받음각이 옆 미끄러워 짐 각으로 바뀐 것이죠.
여기서 비행기에 대한 물리적 이해를 덧붙여봅시다.
수직 꼬리날개는 주로 대칭형 에어포일을 사용합니다.
그리고 수평비행 시, 옆 미끄럼 짐 각이 거의 모든 비행기에서 0도입니다.
이런 이유는 비행 중에 지속적으로 양력은 필요하지만,
횡력은 필요하지 않기 때문입니다.
대칭형 에어포일의 받음각 혹은 옆 미끄러워 짐 각이 0도라면
양력도, 횡력도 발생하지 않기 때문에 깔끔하게 대칭형 에어포일을 사용합니다.
그럼 수직 꼬리날개는 왜 있나요?
필요 없지 않나요?
이렇게 말씀하실 수도 있습니다.
공기가 만약 계속 균일하게 불어온다면 필요 없을 것입니다.
하지만 공기의 방향은 예측 불가하여
안정성을 이유로 존재하는 것이 바로 수직 꼬리날개입니다.
만약 옆 미끄러워짐각으로 바람이 불어온다면
수직 꼬리날개에서 횡력이 작용하게 되어 바람의 방향으로 비행기의 헤딩 각도를 맞춰줍니다.
바람이 불어오는 방향으로 비행기의 헤딩 각도를 맞춰주는 것은 곧 수평비행상태로
비행기가 되돌아가려고 하는 성질을 갖는다는 의미입니다.
마지막으로 수평 꼬리날개의 엘리베이터는 양력을 증가시키거나 감소시켰다면
수직 꼬리날개의 러더(Rudder)는 같은 원리로 횡력(Side force)을 증가시키거나 감소시켜서 비행기의 머리 각도(heading angle)를 좌우로 조절합니다.
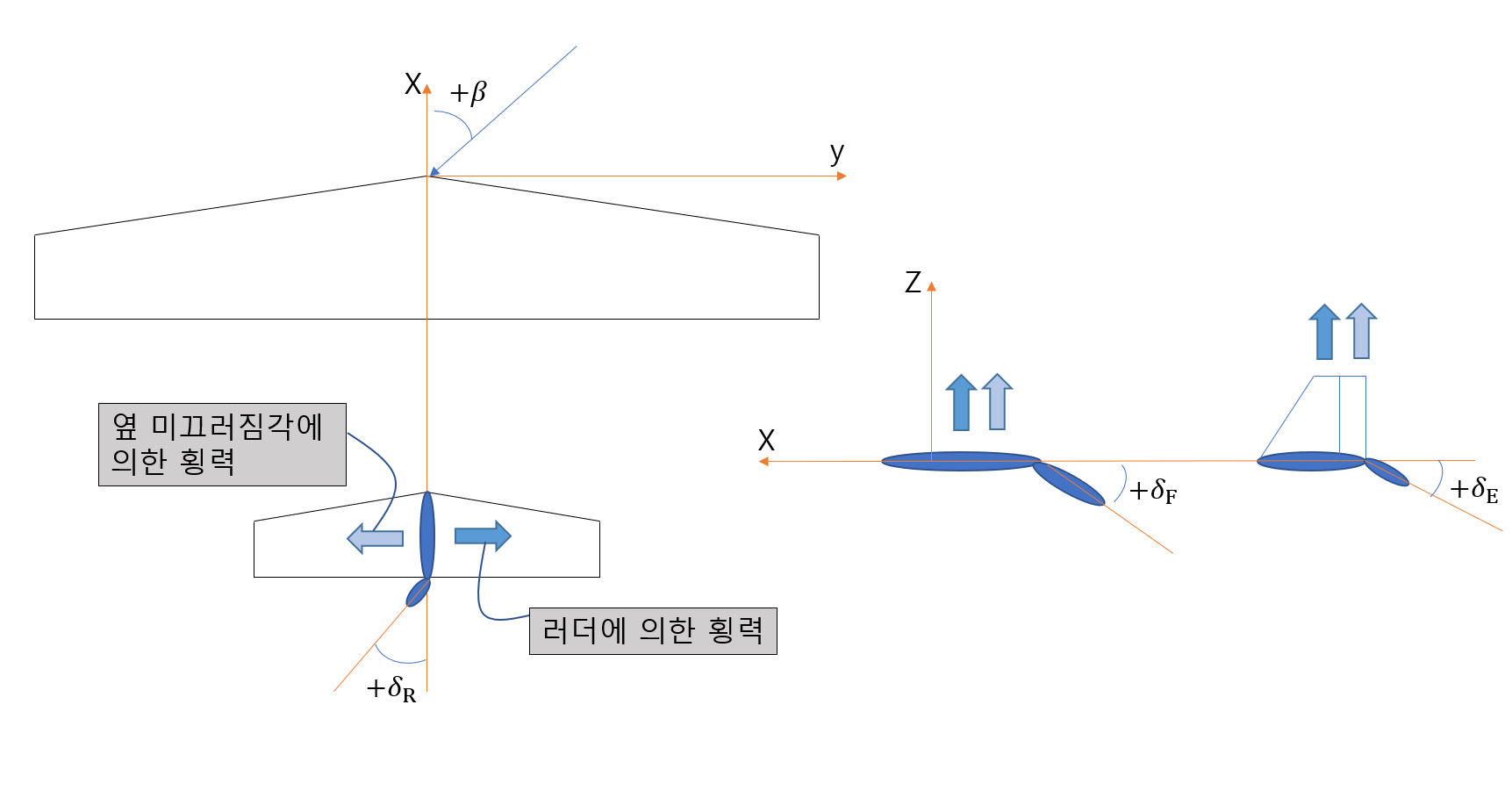
주의해야할 사항이 있습니다.
주날개의 경우와 다르게
수직 꼬리날개는 옆미끄러짐각에 영향으로 인한 횡력의 벡터가 -값을 가지지만
러더의 움직임으로 인한 횡력의 벡터는 +값을 가집니다.
이로 인하여 데체 러더 횡력효과는 -값을 가집니다.
20. 수직 꼬리날개 도식적 특징 추출

일단 이 자료를 보고 저는 혼돈의 카오스로 빠졌습니다.
왜냐면 Aspect ratio도 taper ratio도 없습니다.
그리고 그나마 있는 날개면적도 수평 꼬리날개 위로만 존재하기 때문에
정확한 예측이 심히 힘들 것 같습니다.
어쨌든 가지고 있는 NAVION rc비행기 도면도 있고 하니...
최대한 저 익면적에 맞추어 계산해야겠습니다.
참고로 Fin offset은 수직 꼬리날개의 incidence angle이라고 생각하시면 됩니다.
2도가 들어가 있습니다.
보통 수직 꼬리날개에는 incidence angle이 0도이지만
NAVION은 달랐습니다.
그나마 다행인 것은 에어포일이 대칭형이라는 것입니다.
저는 Root의 에어포일을 NACA0012로 사용하도록 하겠습니다.
너무 복잡해 지기 때문에 어쩔 수 없습니다. ㅠㅠ
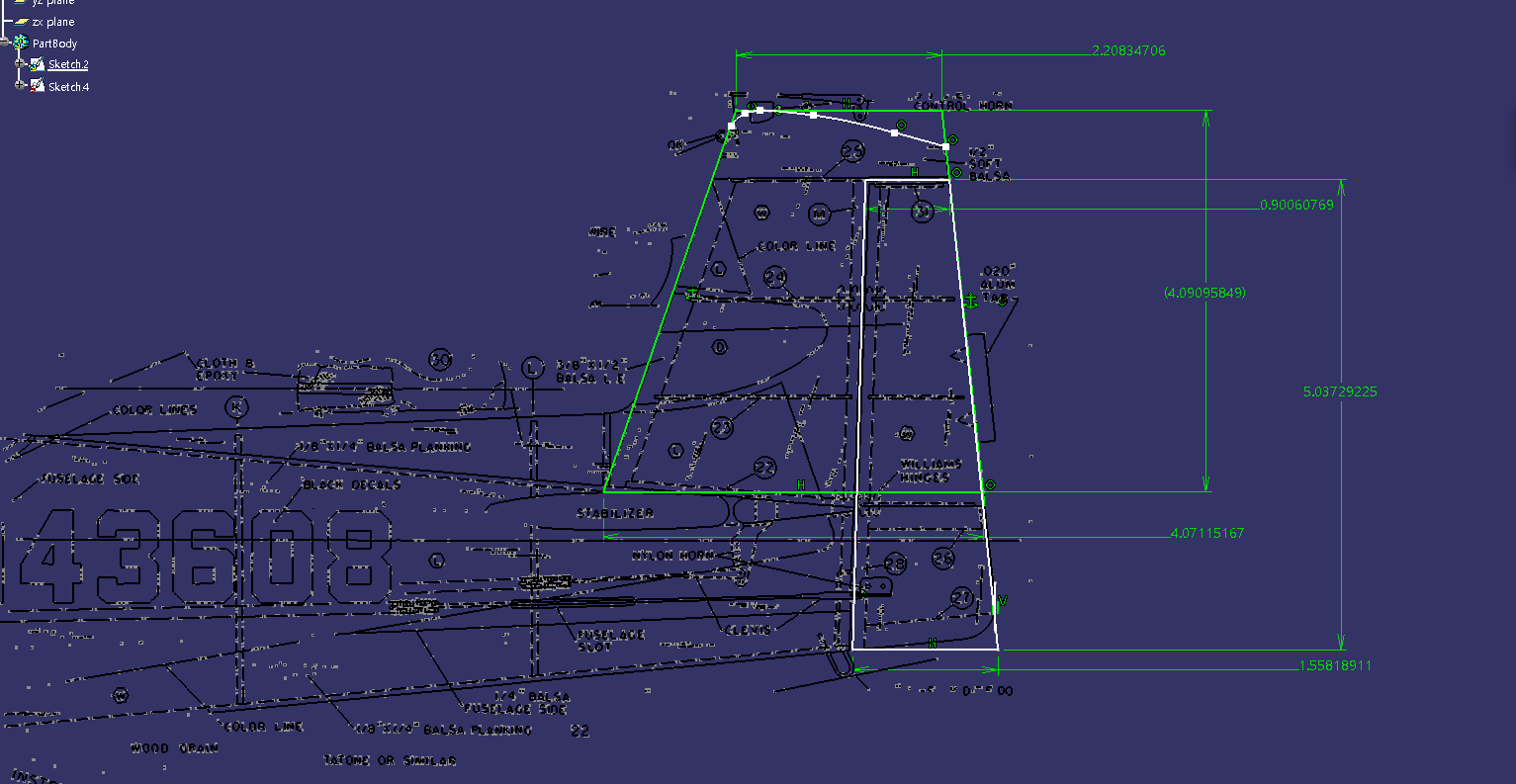

그림 32를 기억하시나요?
제가 프로젝트 초반부에 말씀드렸던 NAVION scale rc 비행기입니다.
이 비행기 도면도 참고용으로 계속 보고 있었습니다.
그림 31을 보시면 이 비행기의 도면을 실제 사이즈로 확대하여 수직 꼬리날개의 특징들을
뽑아내고 있는 것을 확인하실 수 있습니다.
놀랍게도 이 도면은 정확했습니다.
그림 30의 NASA의 수직 꼬리날개 면적을 보시면 12.5$ {ft}^{2}$인 것을 확인하실 수 있습니다.
실제로 계산해보니 면적은 정확히 12.5였습니다.
뿐만 아니라
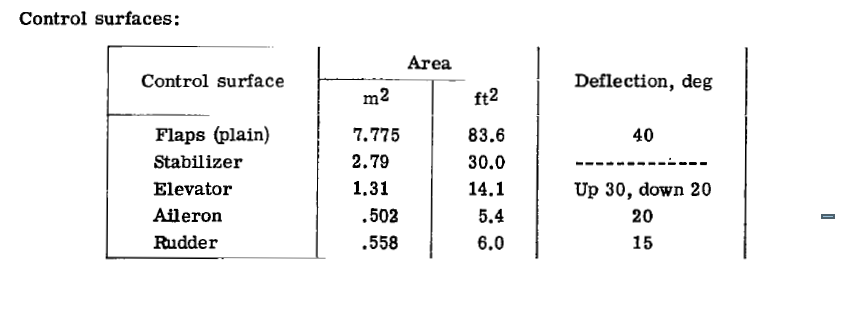
그림 33을 보시면 러더의 면적은 6$ {ft}^{2}$인 것을 확인하실 수 있습니다.
실제로 계산해보니 정확했습니다.
다만 이 면적은 사다리꼴 형태의 면적이 아닌 winglet을 포함한 면적입니다.
우리는 그 면적의 손실은 무시하고 계산하겠습니다.
하지만 실제 제작에서는 모든 winglet을 포함할 것입니다.
제 생각에 공력특성의 큰 차이는 없을 것 같습니다.
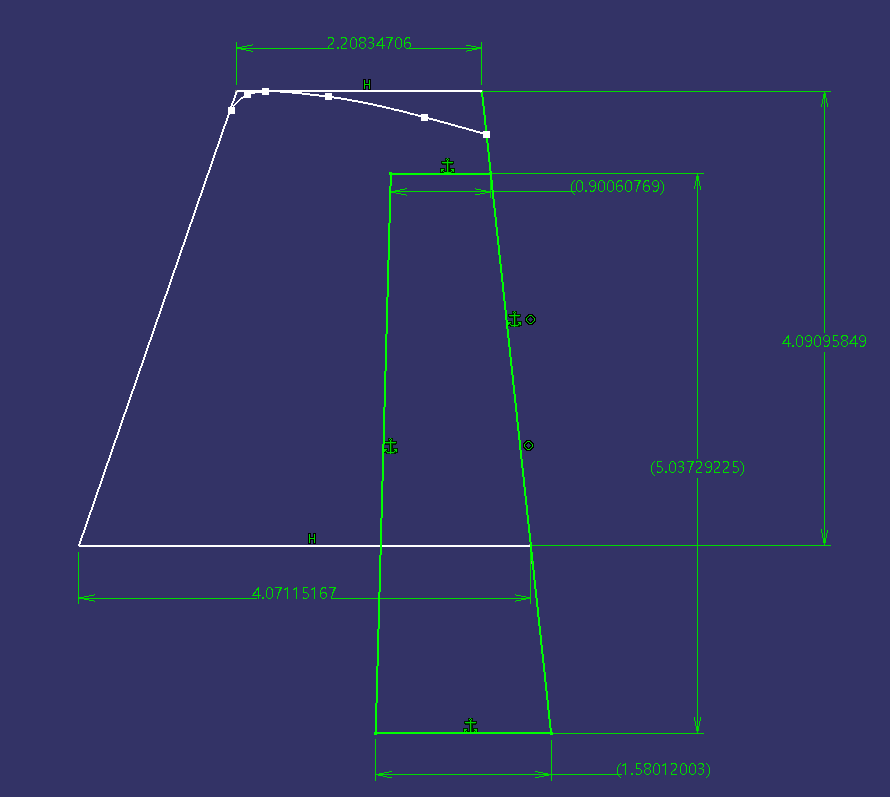
${ C }_{ t }\quad =\quad 2.2083ft$
${ C }_{ r }\quad =\quad 4.0711ft$
${ b }_{ v }\quad =\quad 4.0909ft$
$$c\left( y \right) =4.0711-0.4553y$$ |
(106) |
$$A=\frac { { { b }^{ 2 } } }{ { { S }_{ V } } } =\frac { { { 4.0909 }^{ 2 } } }{ 12.844 } \approx 1.3029$$ |
(107) |
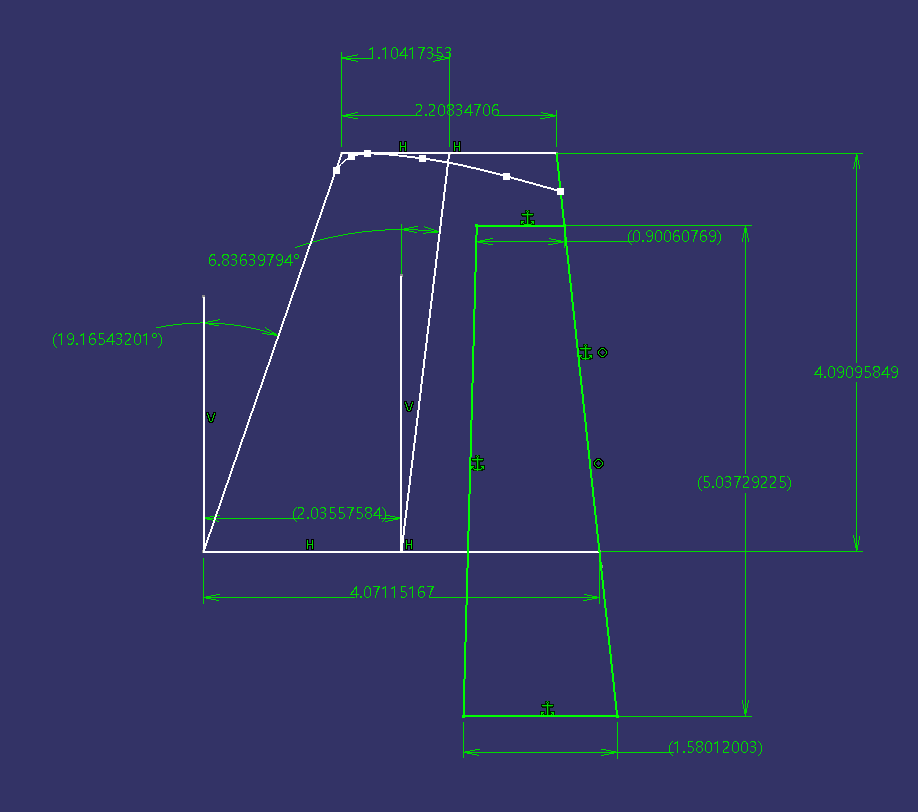
21. 3차원 수직 꼬리날개 횡략선 기울기 구하기
${ { \Lambda }_{ c/2 } }=6.836deg$ |
(108) |
$${ { C }_{ { { S }_{ \beta } } } }=\frac { 2\pi A }{ 2+\sqrt { \frac { { { A }^{ 2 } }{ { \beta }^{ 2 } } }{ { { \kappa }^{ 2 } } } \left( 1+\frac { { { \tan }^{ 2 } }\left( { { \Lambda }_{ c/2 } } \right) }{ { { \beta }^{ 2 } } } \right) +4 } } (/rad)$$ |
(109) |
양력선 기울기와 마찬가지로 횡력선 기울기(Sideforce effectiveness)는 식 108과 같습니다.
※ 주의할 사항 : 여기의 $\beta$ 는 Prandtl-Glauert subsonic compressibility factor입니다
표. 10 마하수에 따른 수직 꼬리날개의 횡력선 기울기
${ M }_{ \infty }=0.01$ |
${ M }_{ \infty }=0.1$ |
${ M }_{ \infty }=0.2$ |
$\beta=0.999$ |
$\beta=0.995$ |
$\beta=0.980$ |
${ C }_{ { S }_{ \beta } }=-1.867\quad (/rad)$ |
${ C }_{ { S }_{ \beta } }=-1.869\quad (/rad)$ |
${ C }_{ { S }_{ \beta } }=-1.873\quad (/rad)$ |
22. 3차원 수직 꼬리날개 양력이 발생하지 않는 옆 미끄러워 짐 각 구하기
※ 주의할 사항 : 여기의 $\beta$ 는 sideslip(옆 미끄러워 짐 각)입니다.
수직 꼬리날개의 incidence angle은 +2도입니다.
$${ { \beta }_{ { { 0 }_{ \, Vtail } } } }=\frac { 1 }{ 12.844 } \int _{ 0 }^{ 4.0909 }{ \left( 0-\left( 2deg \right) \right) \left( 4.0711-0.4553y \right) dy } $$ |
(110) |
$${ { \beta }_{ { { 0 }_{ \, Vtail } } } }=-2.0001deg$$ |
(111) |
23. 3차원 수직 꼬리날개 평균 공력 시위(MAC)와 그 위치 찾기
$$\overline{c}=\frac{1}{{{S}_{w}}}\int\limits_{0}^{b}{{{c}^{2}}dy}=\frac{1}{12.844}\int\limits_{0}^{4.0909}{{{\left( 4.0711-0.4553y \right)}^{2}}dy}$$ |
(112) |
$$\overline{c}=3.2321$$ |
(113) |
$${ { x }_{ LE } }\left( y \right) =0.3475y$$ |
(114) |
$${ { X }_{ L{ { E }_{ MAC } } } }=\frac { 1 }{ 12.844 } \int _{ 0 }^{ 4.0909 }{ 0.3475y\left( 4.0711-0.4553y \right) dy }$$ |
(115) |
$${ { X }_{ L{ { E }_{ MAC } } } }=0.64057ft$$ |
(115) |
$${ { X }_{ A{ { C }_{ Vtail } } } }=\, { { X }_{ L{ { E }_{ MAC } } } }+0.25\overline { c } =1.4486ft$$ |
(116) |
$${ { Z }_{ MAC } }=\frac { 1 }{ 12.844 } \int _{ 0 }^{ 4.0909 }{ y\left( 4.0711-0.4553y \right) dy =3.0721ft}$$ |
(117) |
$${ { Z }_{ MAC } }=1.8433ft$$ |
(118) |
표. 11 수직 꼬리날개의 평균 공력 시위(MAC)와 공력중심의 위치
${ { X }_{ L{ { E }_{ MAC } } } }$ |
${ { Z }_{ MAC } }$ |
${ { X }_{ A{ { C }_{ Vtail } } } }$ |
$\, { 0 }{ .64057 }ft$ |
$1.8433ft$ |
$1.4486ft$ |
24. 수직 꼬리날개의 러더(Rudder) 특징들
러더 횡력 효과(Rudder sideforce effectiveness)는 앞서 말씀드렸다시피
플랩 양력 효과, 엘리베이터 양력 효과랑 같습니다.
다만 날개가 한쪽만 부터있으니까 2/면적에서 2가 아니라 1로 바꿔주시면 됩니다.
$${ { C }_{ { { S }_{ \delta R } } } }=\frac { 1 }{ S } \int _{ { { \eta }_{ i } } }^{ { { \eta }_{ o } } }{ { { C }_{ { { l }_{ \delta } } } }\left( y \right) c\left( y \right) dy }$$ |
(119) |
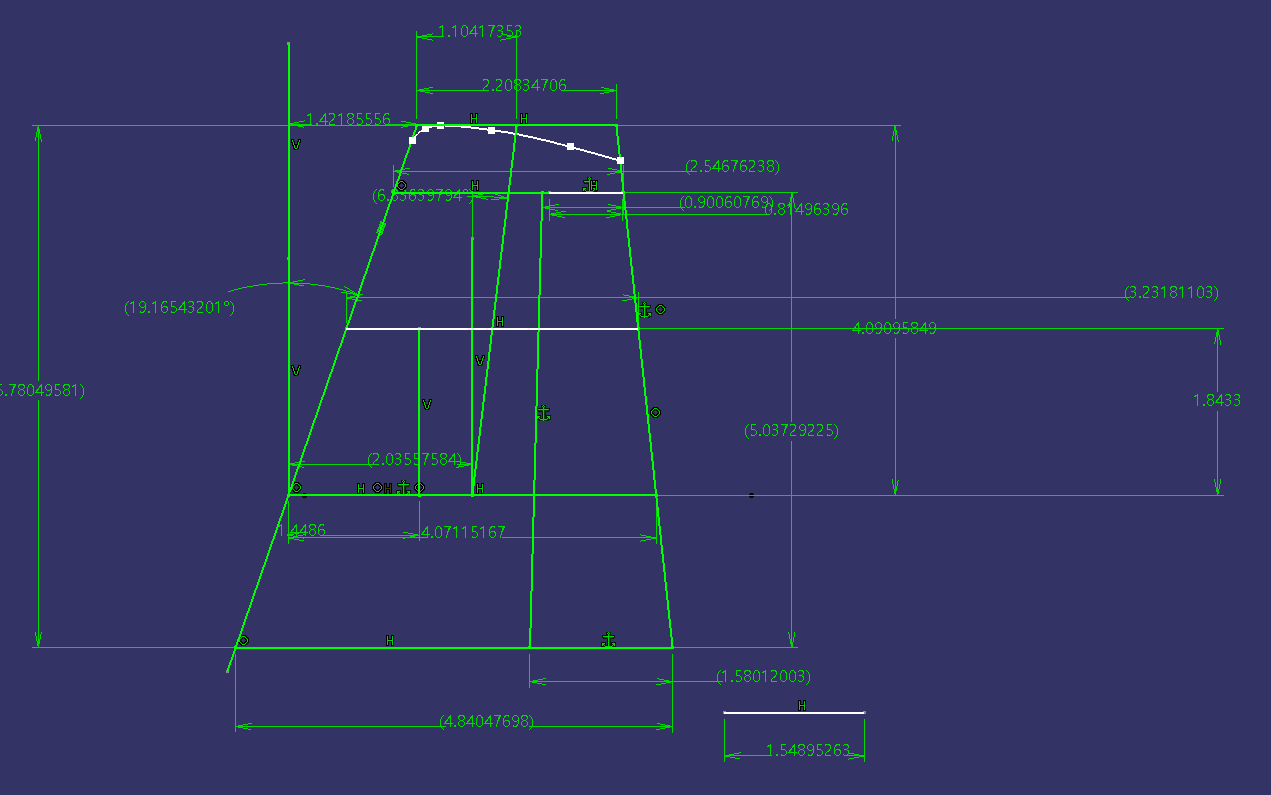
$$c\left( y \right) =4.8404-0.4553y$$ |
(120) |
수평 꼬리날개 위의 면적만 수직 꼬리날개의 면적이었습니다.
실제로 수평 꼬리날개 아래로는 수직 꼬리날개가 아닌 비행기 동체입니다.
하지만 러더는 수평 꼬리날개 아래까지 내려와 있습니다.
airfoil은 같은 NACA0012 임으로
약간의 트릭을 사용해야 합니다.
여기서는 위에서 정리한 수평 꼬리날개의 특징들을 그대로 사용하여
동체를 포함한 수직 꼬리날개를 만들어서 해석하는 게 가장 정확할 것 같습니다.
따라서 날개 면적도 커지고 시위(chord length) 함수도 바뀝니다.
하지만 sweep angle과 aspect ratio, taper ratio, airfoil, incidence는 같습니다.
아이디어 좋죠? ㅋㅋ
$$\frac { { { c }_{ f } } }{ c } =0.35$$ |
(121) |
자 이렇게 되면 실질적으로 많은 부분이 수평 꼬리날개와 같습니다.
시위 함수와 러더 크기만 다를 뿐입니다.
그래프 보고 구한 계수들은 같습니다 ㅋ
$$\begin{align} & { { C }_{ { { S }_{ \delta R } } } }(Rudder)=\frac { 1 }{ S } \int _{ { { \eta }_{ i } } }^{ { { \eta }_{ o } } }{ { { C }_{ { { l }_{ \delta } } } }\left( y \right) c\left( y \right) dy } \\ & =\frac { 1 }{ 20.3722f{ { t }^{ 2 } } } \int _{ 0ft }^{ 5.037ft }{ 4.7959\left( /rad \right) \left( 4.8404-0.4553y \right) }dy \\ & =4.3799\left( /rad \right) \\ & \end{align}$$ |
(122) |
$${ { \beta }_{ \delta } }\left( Rudder \right) \triangleq \frac { { { C }_{ { { S }_{ \delta R } } } } }{ { { C }_{ { { S }_{ \beta } } } } } =\frac { 4.3799/rad }{ -1.873/rad } =-2.3384$$ |
(123) |
표. 12 러더 각도에 따른 계수들
러더 각도 : 10 (deg) |
러더 각도 : 20 (deg) |
러더 각도 : 30 (deg) |
$$\Delta { { C }_{ { { d }_{ flap } } } }=0.016$$ |
$$\Delta { { C }_{ { { d }_{ flap } } } }=0.046$$ |
$$\Delta { { C }_{ { { d }_{ flap } } } }=0.105$$ |
$$\frac { \Delta { { c }_{ { { d }_{ flap } } } } }{ \Delta { { \delta }_{ flap } } } ={ 0 }{ .0917 }/rad$$ |
$$\frac { \Delta { { c }_{ { { d }_{ flap } } } } }{ \Delta { { \delta }_{ flap } } } ={ 0 }{ .1318 }/rad$$ |
$$\frac { \Delta { { c }_{ { { d }_{ flap } } } } }{ \Delta { { \delta }_{ flap } } } ={ 0 }{ .2005 }/rad$$ |
$${ { C }_{ { { D }_{ \delta E } } } }=0.0837/rad$$ |
$${ { C }_{ { { D }_{ \delta E } } } }=0.1204/rad$$ |
$${ { C }_{ { { D }_{ \delta E } } } }=0.1831/rad$$ |
25. 비행기 다운워시의 영향
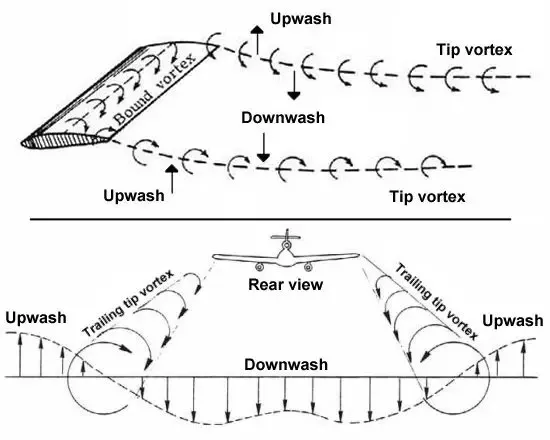
그림 37는 다운워시(Downwash)에 대한 설명을 다루고 있습니다.
부족한 지식으로 나마 설명드리겠습니다.
그림 37의 첫번째 그림은 다운워시의 원리를 말합니다.다운워시는 날개끝 와류로 인하여 공기가 날개끝에서 안쪽으로 말아들어가려는 성질때문에 생기는 공기의 흐름입니다.
아래그림을 보시면 가운데 활처럼 휘어있는 공기를 보실수 있습니다.이는 주날개 뒷전이후로 생기는 공기변화입니다.
이걸 왜 알아야하나요?그 이유는 주 날개 뒤에 있는 수평꼬리날개의 받음각의 변화때문입니다.주 날개가 뀐 방귀를 수평꼬리날개가 그대로 맡아야하는 엽기적인 상황입니다.이로 인하여 수평꼬리날개의 받음각은 감소하게 됩니다.이를 알아야 수평꼬리날개의 양력을 예측할 수 있습니다.
$${ { \alpha }_{ H } }={ { \alpha }_{ W } }+\Delta { { i }_{ H } }-{ { \varepsilon }_{ H } }$$ |
(124) |
다운워시때문에 수평 꼬리날개의 받음각은 식 124로 바뀌게 됩니다.
주의※ : $\varepsilon$는 다운워시 각입니다.
i는 incidence angle입니다.
$${ { \left. \frac { d\varepsilon }{ d{ { \alpha }_{ W } } } \right| }_{ theroy } }=\left\{ \begin{matrix} 1\, \xrightarrow { { } } wing\, trailing\, edge \\ { } \\ \frac { 2{ { C }_{ { { L }_{ { { \alpha }_{ W } } } } } } }{ \pi { { A }_{ W } } } \xrightarrow { { } } infinity\, behind\, wing \\ \end{matrix} \right\} $$ |
(125) |
윗 식은 Downwash gradient를 나타냅니다.
주 날개 뒷전에서는 1이지만, 이 다운워시가 무한히 멀리가면 두번째 식이 됩니다.
$$\varepsilon =\frac{d\varepsilon }{d{{\alpha }_{W}}}\left( {{\alpha }_{W}}-{{\alpha }_{{{0}_{W}}}} \right)$$ |
(126) |
다운워시가 날개의 받음각에 선형적으로 변화한다면 수평 꼬리날개의 다운워시 각도는 위 식과 같습니다.
$${ { \alpha }_{ H } }=\left( 1-\frac { d{ { \varepsilon }_{ H } } }{ d{ { \alpha }_{ W } } } \right) { { \alpha }_{ W } }+\Delta { { i }_{ H } }$$ |
(127) |
수평꼬리 날개의 받음각의 선형적 표현입니다.
뭐 그렇습니다.
위의 식들을 이용해서 여러가지 값들을 구할 수있지만
다 생략하고 수평꼬리날개의 받음각을 알아봅시다.
$${ { \left. \frac { d\varepsilon }{ d{ { \alpha }_{ W } } } \right| }_{ theroy } }=\frac { 2{ { C }_{ { { L }_{ { { \alpha }_{ W } } } } } } }{ \pi { { A }_{ W } } } =\frac { 2\times 4.468 }{ 3.14\times 6.06 } ={ 0 }{ .4694 }$$ |
(128) |
$$\frac { 2{ { l }_{ 2 } } }{ b } =\frac { { { l }_{ 2 } } }{ b/2 } =\frac { 9.2473097 }{ 16.7 } =0.554$$ |
(129) |
$$\frac { 2{ { l }_{ 2 } } }{ b } =\frac { { { l }_{ 2 } } }{ b/2 } =\frac { 153131 }{ 16.7 } =51561$$ |
(130) |
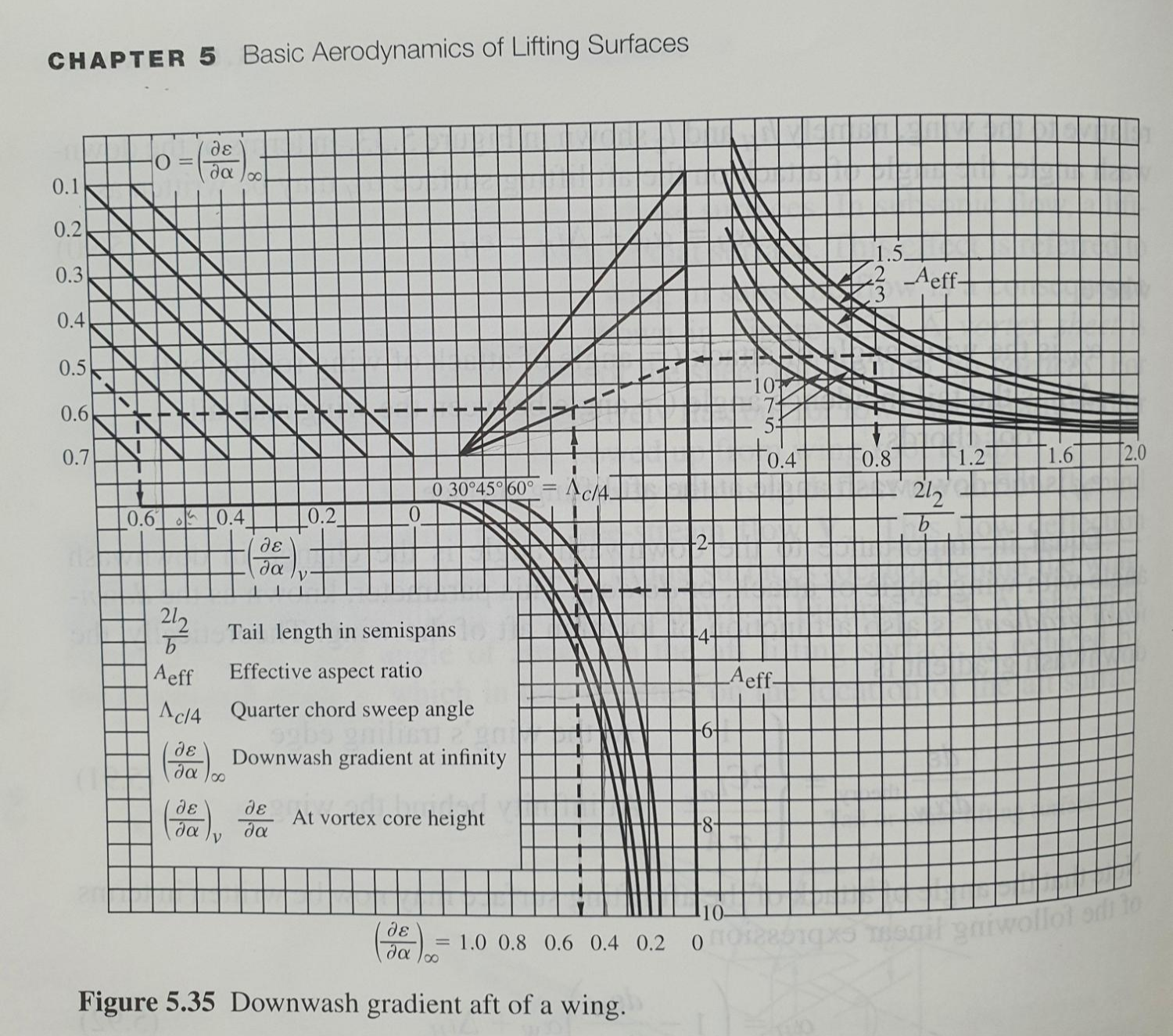
그림 39는 수평 꼬리날개의 앞전에서 다운워시 각도를 알 수 있는 그래프입니다.
절차는 오른쪽 위의 그래프부터 시작하시면 됩니다.
${A}_{eff}$는 주날개의 aspect ratio이고 NAVION의 경우 6.06입니다.
아래축은 위 129식에서 구한 0.554입니다.
이 값들이 겹치는 지점을 찾았다면 수평하게 옆 그래프로 이동합니다.
세로축도 aspect ratio, 6.06임이고 mid-sweep angle은 약 2.6도로 매우작습니다.
거기에 해당하는 지점을 찾았다면 위로 올라가서
여러 선이 겹치는 원점을 기준으로 대각선을 가까 수평하게 이어온 값과 이어
아래에서 수직하게 올라오는 값과 교차시키고 다시 오른쪽 그래프로 이동합니다.
그럼 식 128에서 구한 무한대에서 다운워시 변화량인 0.46에 해당하는 대각선까지
수평하게 아까 값을 가져와서 아래로 내리면
우리가 원하는 수평 꼬리날개에서 다운워시 변화량을 알 수있습니다.
$$\frac { d\varepsilon }{ d{ { \alpha }_{ W } } } =0.56$$ |
(131) |
그럼 식 131의 값을 구하실 수 있습니다.
이 값은 수평꼬리날개에서 받음각에 대한 다운워시각의 변화량이다.
$${\varepsilon}_{H}= 0.56(비행기 받음각-(-4.95)) $$ |
(132) |
식 132는 식 126을 위에서 구한 값들로 정리한 것입니다.
비행기의 받음각만 알면 다운워시각을 구할 수 있습니다.
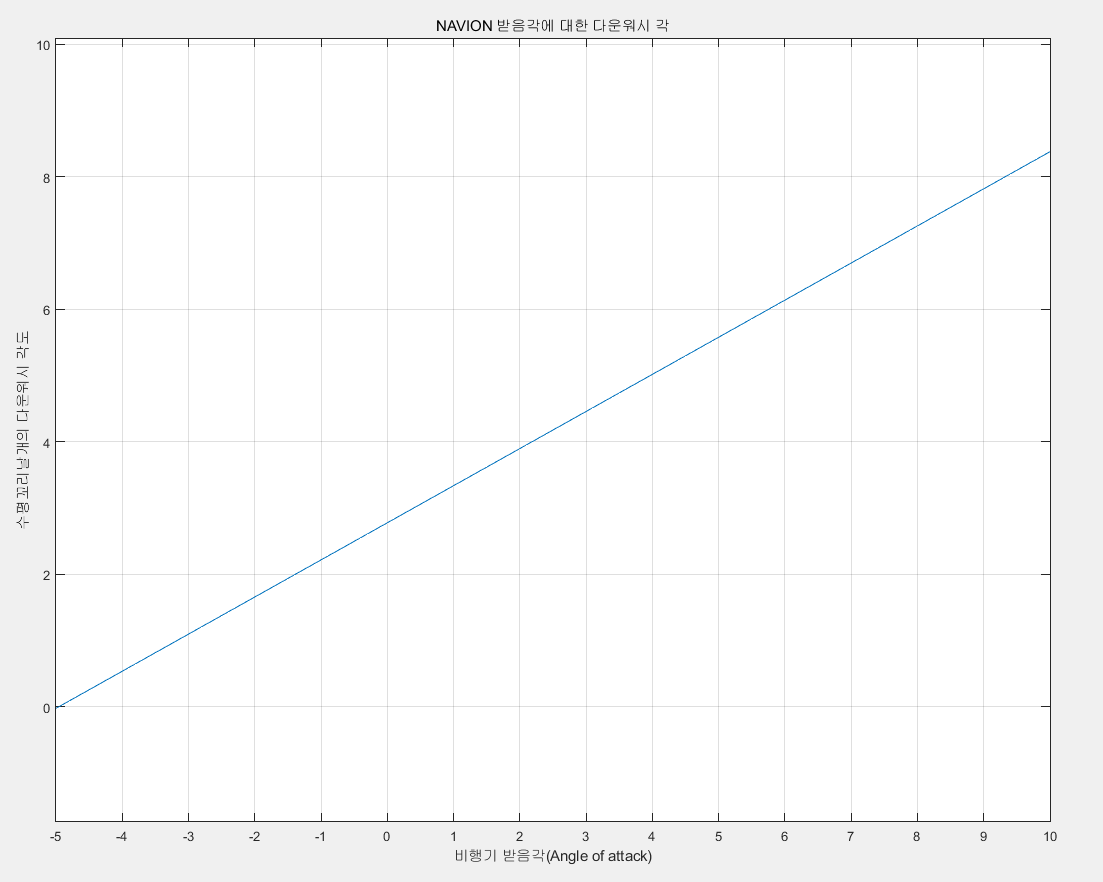
그림 40은 식 132를 그래프로 만든 것입니다.
나중에 비행기 시뮬레이션을 할때 유용하게 사용될 것같습니다.
비행기 트림조건에 대한 받음각이 다르니까요.
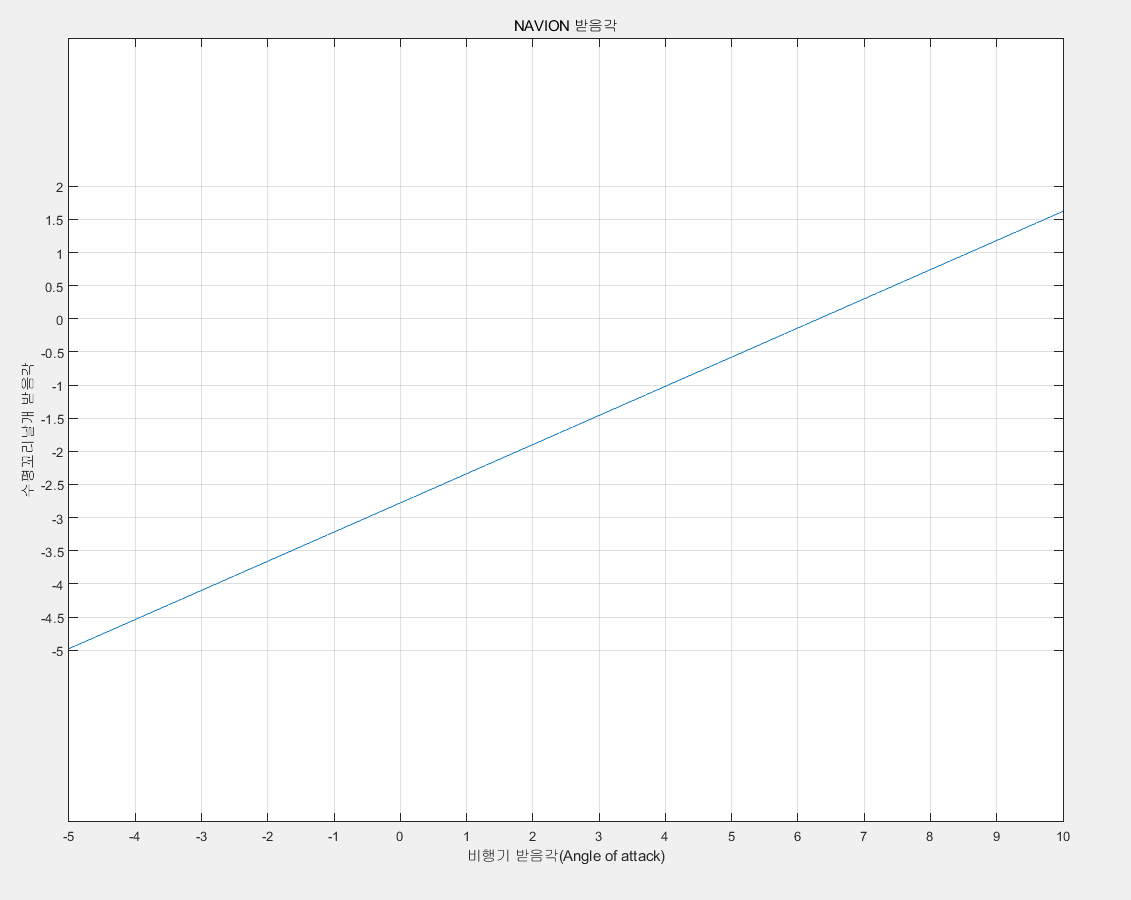
다운워시 영향을 고려한 수평꼬리날개의 받음각은 위와 같습니다.
이는 지금까지 구한값을 식 124에 대입한 결과입니다.
수평 꼬리날개의 incidence 각도는 0도로 하였습니다.
여기까지 수직 꼬리날개의 해석을 해봤습니다.
여기서 사용되는 값들은 모두 앞으로 등장할 계획입니다.
회 뜨기 전에 물고기 및 재료 손질이라고나 할까요? ㅋㅋ
여러 안정성... 시뮬레이션.... 등등을 분석하기 위한 사전 작업이었습니다.
'비행기 설계' 카테고리의 다른 글
| [프로젝트1-28] NAVION의 공기력 (0) | 2020.08.22 |
|---|---|
| [프로젝트1-27] 지금까지 구한 계수들 정리 (0) | 2020.08.20 |
| [프로젝트1-25] 3차원 꼬리날개 분석 (0) | 2020.08.09 |
| [프로젝트1-24] 주익 조종면 해석 2 (0) | 2020.08.04 |
| [프로젝트1-23] 주익 조종면 해석 (4) | 2020.08.04 |
