티스토리 뷰

지금까지 비행기의 공기력을 해석하기 위한 많은 계수들을 정리했습니다.
이제부터 비행기의 공기력을 정리하겠습니다.
26. 비행기의 양력(Lift)
$$\begin{align} & { { C }_{ L } }={ { C }_{ { { L }_{ { { \alpha }_{ W } } } } } }\left( { { \alpha }_{ W } }+{ { i }_{ W } }-{ { \alpha }_{ { { 0 }_{ W } } } } \right) \\ & +{ { C }_{ { { L }_{ H } } } }\frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ H } } }{ { { S }_{ W } } } \left( \left( 1-\frac { d\varepsilon }{ d\alpha } \right) { { \alpha }_{ W } }-\frac { d\varepsilon }{ d\alpha } \left( { { i }_{ W } }-{ { \alpha }_{ { { 0 }_{ W } } } } \right) +{ { i }_{ H } }-{ { \alpha }_{ { { 0 }_{ H } } } }+{ { \alpha }_{ \delta } }{ { \delta }_{ E } } \right) \\ & \end{align}$$ |
(133) |
비행기의 양력은 거의 99% 주날개와 수평 꼬리날개에서 발생합니다.
그래서 비행기 전체의 양력 계수는 위와 같습니다.
이 값은 다운 워시의 영향을 포함합니다.
$${ { C }_{ { { L }_{ \alpha } } } }={ { C }_{ { { L }_{ { { \alpha }_{ W } } } } } }+{ { C }_{ { { L }_{ { { \alpha }_{ H } } } } } }\left( 1-\frac { d\varepsilon }{ d{ { \alpha }_{ W } } } \right) \frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ H } } }{ { { S }_{ W } } }$$ |
(134) |
식 133은 비행기 전체의 양력입니다.
이를 비행기의 받음각으로 미분하면 식 134가 나옵니다.
이를 비행기 받음각 양력 효과(Vehicle angle of attack lift effectiveness)라고 합니다.
비행기 양력 계수의 기울기인 거죠
$${ { C }_{ { { L }_{ \delta E } } } }={ { C }_{ { { L }_{ { { \alpha }_{ H } } } } } }{ { \alpha }_{ \delta } }\frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ H } } }{ { { S }_{ W } } }$$ |
(135) |
식 135는 식 133을 엘리베이터 각도로 미분한 값입니다.
이를 엘리베이터 양력 효과(Elevator lift effectiveness)라고 합니다.
${\alpha}_{\delta}$는 수평 꼬리날개의 대체 플랩 양력 계수입니다.
$${ { C }_{ { { L }_{ { { i }_{ H } } } } } }={ { C }_{ { { L }_{ { { \alpha }_{ H } } } } } }\frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ H } } }{ { { S }_{ W } } }$$ |
(136) |
식 136은 식 133을 수평 꼬리날개의 incidence 각으로 미분한 값입니다.
이를 꼬리 붙임각 양력 효과(tail-incidence lift effectiveness)라고 합니다.
$$\begin{align} & { { \left. { { C }_{ L } } \right| }_{ \alpha =\delta E={ { i }_{ H } }=0 } }={ { C }_{ { { L }_{ { { \alpha }_{ W } } } } } }\left( { { i }_{ W } }-{ { \alpha }_{ { { 0 }_{ W } } } } \right) \\ & +{ { C }_{ { { L }_{ { { \alpha }_{ H } } } } } }\left( -\frac { d\varepsilon }{ d\alpha } \left( { { i }_{ W } }-{ { \alpha }_{ { { 0 }_{ W } } } } \right) -{ { \alpha }_{ { { 0 }_{ H } } } } \right) \frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ H } } }{ { { S }_{ W } } } \\ & \end{align}$$ |
(137) |
식 137은 받음각, 엘리베이터 각, 수평 미익 붙임각이 0일 때 양력 계수를 나타냅니다.
종종 이 상황에도 양력이 0이 아닙니다.
이 또한 양력의 기준이 됩니다.
27. 비행기의 횡력(Sideforce)
$${ { C }_{ S } }={ { C }_{ { { S }_{ Vtail } } } }\frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ V } } }{ { { S }_{ W } } } ={ { C }_{ { { S }_{ { { \beta }_{ Vtail } } } } } }\left( \beta +{ { \beta }_{ \delta } }{ { \delta }_{ R } } \right) \frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ V } } }{ { { S }_{ W } } }$$ |
(138) |
식 138은 비행기의 횡력 계수입니다.
비행기의 99%의 횡력은 수직 꼬리날개에서 발생합니다.
물론 러더의 영향도 포함됩니다.
$${ { C }_{ { { S }_{ \beta } } } }={ { C }_{ { { S }_{ { { \beta }_{ Vtail } } } } } }\frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ V } } }{ { { S }_{ W } } }$$ |
(139) |
식 139는 비행기의 횡력 계수(식 138)를 옆 미끄러워짐각으로 미분한 값입니다.
이를 비행기 옆미끄러짐각 횡력 효과(Vehicle's sideslip side-force effectiveness)라고 합니다.
$${ { C }_{ { { S }_{ \delta R } } } }={ { C }_{ { { S }_{ { { \beta }_{ Vtail } } } } } }{ { \beta }_{ \delta } }\frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ V } } }{ { { S }_{ W } } }$$ |
(140) |
식 140은 비행기의 횡력 계수를 러더 각도 미분한 것입니다.
이를 비행기 러더 횡력 효과(Vehicle's rudder sideforce effectiveness)라고 합니다.
28. 비행기의 항력(Drag)
$$\begin{align} & D={ { D }_{ W } }+{ { D }_{ H } }+{ { D }_{ V } }+{ { D }_{ F } } \\ & ={ { C }_{ { { D }_{ W } } } }{ { q }_{ \infty } }{ { S }_{ W } }+{ { C }_{ { { D }_{ H } } } }{ { q }_{ \infty } }{ { S }_{ H } }+{ { C }_{ { { D }_{ V } } } }{ { q }_{ \infty } }{ { S }_{ V } }+{ { C }_{ { { D }_{ F } } } }{ { q }_{ \infty } }{ { S }_{ F } } \\ & ={ { C }_{ D } }{ { q }_{ \infty } }{ { S }_{ W } } \\ & \end{align}$$ |
(141) |
비행기의 항력은 주날개, 수평 꼬리날개, 수직 꼬리날개, 동체에서 99% 발생합니다.
그걸 식 141로 표현한 것입니다.
$$\begin{align} & { { C }_{ D } }=\left( { { C }_{ { { D }_{ { { 0 }_{ W } } } } } }+{ { C }_{ { { D }_{ F } } } }\frac { { { S }_{ F } } }{ { { S }_{ W } } } +{ { C }_{ { { D }_{ { { 0 }_{ H } } } } } }\frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ H } } }{ { { S }_{ W } } } +{ { C }_{ { { D }_{ { { 0 }_{ V } } } } } }\frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ V } } }{ { { S }_{ W } } } \right) \\ & +\left( \frac { C_{ { { L }_{ W } } }^{ 2 } }{ \pi { { A }_{ W } }{ { e }_{ W } } } +\frac { C_{ { { L }_{ H } } }^{ 2 } }{ \pi { { A }_{ H } }{ { e }_{ H } } } \frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ H } } }{ { { S }_{ W } } } +\frac { C_{ { { S }_{ Vtail } } }^{ 2 } }{ \pi { { A }_{ V } }{ { e }_{ V } } } \frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ V } } }{ { { S }_{ W } } } \right) \\ & \end{align}$$ |
(142) |
식 142는 비행기의 항력 계수입니다.
첫 번째 괄호를 주로 유해 항력 집단(Parasite drag set)이라고 하며
하첨자 0이 있는 계수들은 유해 항력을 의미합니다.
이는 저번 보고서 3에서 구하는 법을 다루었습니다.
비행기의 트림 조건에 해당하는 항력 계수를 넣어주면 될 것 같습니다.
두 번째 괄호를 유도 항력 집단(Induced drag set)이라고 합니다.
이는 날개 끝에서 발행하는 와류에 의해서 발생하는 항력입니다.
위의 계수들 중 아직 모르는 것은 동체의 항력 계수입니다.
저도 이걸 간과했습니다.
나머지는 다 알고 있지만 동체의 항력 계수는 손으로 구할 수가 없습니다.
이는 XFLR5를 통해서 구하던지 해야 할 것 같습니다.
$${ { C }_{ { { D }_{ \alpha } } } }=\frac { 2 }{ \pi } \left( \frac { { { C }_{ { { L }_{ W } } } } }{ { { A }_{ W } }{ { e }_{ W } } } { { C }_{ { { L }_{ { { \alpha }_{ W } } } } } }+\frac { { { C }_{ { { L }_{ H } } } } }{ { { A }_{ H } }{ { e }_{ H } } } { { C }_{ { { L }_{ { { \alpha }_{ H } } } } } }\frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ H } } }{ { { S }_{ W } } } \left( 1-\frac { d\varepsilon }{ d\alpha } \right) \right) $$ |
(143) |
식 143은 식 142를 받음각으로 미분한 값이다.
이를 비행기 받음각 항력 효과(Vehicle's angle of attack drag effectiveness)라고 합니다.
$${ { C }_{ { { D }_{ \delta E } } } }=\frac { 2{ { C }_{ { { L }_{ H } } } } }{ \pi { { A }_{ H } }{ { e }_{ H } } } { { C }_{ { { L }_{ { { \alpha }_{ H } } } } } }{ { \alpha }_{ \delta } }\frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ H } } }{ { { S }_{ W } } }$$ |
(144) |
식 144는 식 142를 엘리베이터 각도로 미분한 값이다.
이를 비행기 엘리베이터 항력 효과(Vehicle's elevator drag effectiveness)라고 합니다.
$${ { C }_{ { { D }_{ { { i }_{ H } } } } } }=\frac { 2{ { C }_{ { { L }_{ H } } } } }{ \pi { { A }_{ H } }{ { e }_{ H } } } { { C }_{ { { L }_{ { { \alpha }_{ H } } } } } }\frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ H } } }{ { { S }_{ W } } } $$ |
(추가) |
$${ { C }_{ { { D }_{ \beta } } } }=\frac { 2 { { C }_{ { { S }_{ Vtail } } } } }{ \pi { { A }_{ V } }{ { e }_{ V } } } { { C }_{ { { S }_{ { { \beta }_{ Vtail } } } } } }\frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ V } } }{ { { S }_{ W } } }$$ |
(145) |
식 145는 식 142를 옆 미끄러워짐각으로 미분한 값이다.
이를 비행기 옆미끄러짐각 항력 효과(Vehicle's sideslip drag effectiveness)라고 합니다.
$${ { C }_{ { { D }_{ \delta R } } } }=\frac { 2{ { C }_{ { { S }_{ Vtail } } } } }{ \pi { { A }_{ V } }{ { e }_{ V } } } { { C }_{ { { S }_{ { { \beta }_{ Vtail } } } } } }{ { \beta }_{ \delta } }\frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ V } } }{ { { S }_{ W } } }$$ |
(146) |
식 146은 식 142를 러더 각도로 미분한 값입니다.
이를 비행기 러더 항력 효과(Vehicle's rudder drag effectiveness)라고 합니다.
$$\begin{align} & { { \left. { { C }_{ D } } \right| }_{ \alpha =\beta ={ { i }_{ H } }={ { \delta }_{ E } }={ { \delta }_{ R } }=0 } } \\ & ={ { C }_{ { { D }_{ 0 } } } }+\frac { 1 }{ \pi { { A }_{ W } }{ { e }_{ W } } } \left( C_{ { { L }_{ W } } }^{ 2 }+C_{ { { L }_{ H } } }^{ 2 }\frac { { { A }_{ W } }{ { e }_{ W } } }{ { { A }_{ H } }{ { e }_{ H } } } \frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ H } } }{ { { S }_{ W } } } \right) \\ & \end{align}$$ |
(147) |
식 147은 받음각, 옆 미끄러워짐각, 수평 꼬리날개의 붙임각, 엘리베이터각, 러더 각도가 0일 때 항력 계수를 의미합니다. 상식적으로 이러면 항력이 없을 것 같지만 실제로는 항력이 존재합니다.
이는 중요한 기준이 됩니다.
29. 비행기의 피칭 모멘트(Pitching moment)
자 원래는 롤링, 피칭, 요잉 순으로 X, Y, Z 축의 회전운동을 고려하는 게 올바른 순서이지만,
롤링과 요잉은 상대적으로 덜 중요하기 때문에 나중에 계산하겠습니다.
먼저 비행기의 피칭 모멘트를 계산하겠습니다.
왜 비행기의 피칭 모멘트가 중요할까요?
일단 떠야 하지 않겠습니까?
여기서 잠깐 언급하겠습니다.
비행기에는 대표적인 트림조건(Trim condition)이 3가지 존재합니다.
1. 안정 직선 비행 (Steady Rectilinear flight )
2. 안정 턴 비행 (Steady turning flight)
3. 준 안정 풀업 비행 (Quasi-steady pull up)
1. 안정 직선 비행은 말그대로 직선비행입니다.
일정한 속도와 각도로 비행기가 나는 상황이죠
우리가 흔히 아는 수평비행상태입니다.
이는 횡력의 영향을 무시합니다.
따라서 롤링이나 요잉같은 운동은 지금 당장 불필요합니다.
일단 다른 것들도 중요하지만 우선 수평비행시!
받음각은 몇도이고
엘리베이터 각도는 몇도이고
추력은 얼마나 필요한지 계산을 먼저 하려고합니다.
(추력을 알면 속도도 예측가능)
제가 앞에서 어떤 계수는 기준이 된다... 이런식으로 말씀드린게
여러가지 있습니다. 기 기준들을 모아모아 이제는 수평비행이 기준이 됩니다.
그럼 수평비행시에 다른 외란이 없다면 비행기는 계속 그상태를 유지할 것입니다.
그럼 이 비행 상태가 기준인 것이죠
이상태에서 엘리베이터를 더 치면?
고도가 더 올라가겠죠? 그리고 속도는 좀 줄어들 것입니다.
이러이러한 것들을 예측하는 것이 바로 시뮬레이션입니다.
이는 무조건 특정 트림조건에서 분석합니다.
아직 저는 NAVION의 트림조건을 하나도 모르기때문에
(책에 나오긴함.. 비교해보겠습니다)
수평비행상태 즉, 안정 직선 비행상태의 트림 조건을 먼저 구하려고 합니다.
따라서 피칭모멘트까지만 구하고 공기력은 잠시 접어두고 넘어가겠습니다.
참고로 말씀드리자면 비행기의 모멘트를 예측하는 것은 XFLR5만으로 신뢰를 얻기는 어렵습니다.
전문적인 CFD(전산 유체 역학)의 기법을 이용해야 정확하게 예측 할 수 있습니다. (유체역학 석사이상)
그럼 어떡합니까?
이 책에서는 많은 경험식과 선대 과학자들의 지식을 모아모아 수식을 만들어 두었습니다.
가져다가 사용하면 정확할 것입니다.
$${ { M }_{ A } }={ { M }_{ { { 0 }_{ F } } } }+{ { M }_{ { { A }_{ W\& H } } } }$$ |
(148) |
식 148은 비행기 전체의 피칭모멘트를 나타냅니다.
첫번째 계수는 비행기 동체에서 발생하는 피칭모멘트계수이고
두번째 계수는 비행기의 주날개와 수평꼬리날개에서 발생하는 피칭모멘트입니다.
동체에서 발생하는 피칭모멘트는 경험식을 이용하여 구하고
날개의 공기력때문에 발생하는 모멘트는 아래식을 이용해서 구합니다.
$$\begin{align} & { { M }_{ { { A }_{ W\& H } } } }={ { M }_{ A{ { C }_{ W } } } }+\left( { { L }_{ W } }\cos \alpha +{ { D }_{ W } }\sin \alpha \right) \left( { { X }_{ A{ { C }_{ W } } } }-{ { X }_{ CG } } \right) \\ & +\left( -{ { L }_{ W } }\sin \alpha +{ { D }_{ W } }\cos \alpha \right) { { Z }_{ A{ { C }_{ W } } } }+{ { M }_{ A{ { C }_{ H } } } } \\ & -\left( { { L }_{ H } }\cos \alpha +{ { D }_{ H } }\sin \alpha \right) \left( { { X }_{ CG } }-{ { X }_{ A{ { C }_{ H } } } } \right) \\ & +\left( -{ { L }_{ H } }\sin \alpha +{ { D }_{ H } }\cos \alpha \right) { { Z }_{ A{ { C }_{ H } } } } \\ & \end{align}$$ |
(149) |
식 149은 비행기의 주 날개와 수평 꼬리날개에서 발생하는 양력과 항력에 의한 공기력이 비행기의 CG에서 발생하는 모멘트를 정리한 수식입니다.
이 식에서 몇 개의 변수를 지우기위해서
우리는 전통적인 항공기를 가정합니다.
따라서
코사인값이 사인값보다 훨씬 크고(미소 받음각때문에)
양력이 항력보다 훨씬 크고
(수직꼬리날개의 공력중심과 동체 추력선 사이 Z 축 길이)보다 X축 공력중심과 무게중심의 차이가 훨씬 크다는 것을 알고 있습니다.
그리고 꼬리 날개의 경우 거의 대칭형 에어포일을 사용해서 자체 에어포일에 의한 피칭 모멘트는 없습니다.
이렇다면 아래 식처럼 근사시킬 수 있고 손으로 풀 수 있습니다.
$${{M}_{{{A}_{W\& H}}}}={{M}_{A{{C}_{W}}}}+{{L}_{W}}\left( {{X}_{A{{C}_{W}}}}-{{X}_{CG}} \right)-{{L}_{H}}\left( {{X}_{CG}}-{{X}_{A{{C}_{H}}}} \right)$$ |
(150) |
위 식을 우리가 지금까지 구한 값들을 집어넣어 정리하면 아래와 같습니다.
$$\begin{align} & { { M }_{ { { A }_{ W\& H } } } }={ { C }_{ { { M }_{ A{ { C }_{ W } } } } } }{ { q }_{ \infty } }{ { S }_{ W } }\overline { { { c }_{ W } } } +{ { C }_{ { { L }_{ { { \alpha }_{ W } } } } } }\left( \alpha +{ { i }_{ W } }-{ { \alpha }_{ { { 0 }_{ W } } } } \right) \left( { { X }_{ A{ { C }_{ W } } } }-{ { X }_{ CG } } \right) { { q }_{ \infty } }{ { S }_{ W } } \\ & -{ { C }_{ { { L }_{ { { \alpha }_{ H } } } } } }\left( \left( 1-\frac { d\varepsilon }{ d\alpha } \right) \alpha +\frac { d\varepsilon }{ d\alpha } \left( { { \alpha }_{ { { 0 }_{ W } } } }-{ { i }_{ W } } \right) +{ { i }_{ H } }-{ { \alpha }_{ { { 0 }_{ H } } } }+{ { \alpha }_{ \delta } }{ { \delta }_{ E } } \right) \left( { { X }_{ CG } }-{ { X }_{ A{ { C }_{ H } } } } \right) { { q }_{ H } }{ { S }_{ H } } \\ & \end{align} \tag{151} \\$$
이 식 안의 모든 계수들은 우리가 이미 구했습니다.
풀면 끝!
$${ { M }_{ { { o }_{ F } } } }={ { C }_{ { { M }_{ { { o }_{ F } } } } } }{ { q }_{ \infty } }{ { S }_{ W } }{ { \overline { c } }_{ W } }=\frac { \kappa { { q }_{ \infty } }{ { \alpha }_{ { { 0 }_{ W } } } } }{ 36.5 } \sum _{ { { x }_{ i } }=0 }^{ { { x }_{ i } }={ { l }_{ F } } }{ w_{ { { F }_{ i } } }^{ 2 } }\Delta { { x }_{ i } }$$ |
(152) |
위의 수식은 만들어진 동체 0 양력 피칭모멘트(The fuselage- generated zero-lift pitching moment)입니다.
------------------------------------------------------용어 설명----------------------------------------------------
$\kappa $ = 문크 분명한 질량 계수? (Munk apparent - mass term)
${ x }_{ i }$ = 비행기 동체를 머리부터 엉덩이까지 i개의 셀로 나누었을때 i번째 셀까지 x축길이
$\triangle { x }_{ i }$ = 비행기 동체를 머리부터 엉덩이까지 i개의 셀로 나누었을때 i번째 셀의 x축 길이
${ l }_{ F }$ = 전체 동체 길이 (x축)
${ w }_{ { F }_{ i } }$ = i번째 셀의 평균 너비
${ \alpha }_{ { 0 }_{ W } }$ = 주 날개 0양력 받음각
---------------------------------------------------------------------------------------------------------------------
전통적인 항공기에서는 동체의 양력을 무시합니다.
하지만 피칭모멘트는 무시할 수 없습니다.
왜냐하면 동체와 날개가 연결된 부분의 공력중심에 변화가 생기기때문입니다.
이는 주 날개앞의 Upwash, 주 날개뒤의 Downwash의 영향과 밀접한 관련있습니다.
(자세한 설명은 :https://ntrs.nasa.gov/citations/20000004246)
$${ { M }_{ { { \alpha }_{ F } } } }={ { C }_{ { { M }_{ { { \alpha }_{ F } } } } } }{ { q }_{ \infty } }{ { S }_{ W } }\overline { { { c }_{ W } } } \approx \frac { { { q }_{ \infty } } }{ 36.5 } \sum _{ { { x }_{ i } }=0 }^{ { { x }_{ i } }={ { l }_{ F } } }{ w_{ { { F }_{ i } } }^{ 2 } } \frac { d{ { \alpha }_{ local } } }{ d{ { \alpha }_{ W } } } \left( { x }_{ i } \right) \Delta { { x }_{ i } }\left( /deg \right)$$ |
(153) |
------------------------------------------------------용어 설명----------------------------------------------------
${ x }_{ i }$ = 비행기 동체를 머리부터 엉덩이까지 i개의 셀로 나누었을때 i번째 셀까지 x축길이
$\triangle { x }_{ i }$ = 비행기 동체를 머리부터 엉덩이까지 i개의 셀로 나누었을때 i번째 셀의 x축 길이
${ l }_{ F }$ = 전체 동체 길이 (x축)
${ w }_{ { F }_{ i } }$ = i번째 셀의 평균 너비
$\frac { d{ { \alpha }_{ local } } }{ d{ { \alpha }_{ W } } } \left( { { x }_{ i } } \right)$ = ${ x }_{ i }$에서 지역 흐름 각도의 변화량 (Local flow- angle gradient at fuselage location ${ x }_{ i }$)
${{\alpha }_{local}}={{\alpha }_{W}}\pm \varepsilon $ = 날개 단면의 지역 흐름 붙임각 (Local flow-incidence angle of the section)
※주의 : $\varepsilon$ = upwash(downwash) 둘다 가능합니다.
주날개 앞에 셀에 대해서 해석할때는 upwash로 별도로 해당 위치에 대해서 구해줘야하고
주날개 기준 뒤의 셀을 해석할때는 downwash로 별도로 해당 위치에 대해서 구해줘야하합니다.
우리가 저번에 구했던 수평꼬리날개에서 downwash 각도는 수평꼬리날개 위치의 값을 구한 것이고
이건 셀 위치마다 다 구해줘야하는 엄청난 고난의 노가다가 되겠습니다.
---------------------------------------------------------------------------------------------------------------------
식 153은 날개와동체의 결합의 받음각 피칭모멘트 효과(Angle of attack pitching moment effectiveness of the wing-fuselage combination)입니다.
※주의 : 비행기 받음각 피칭모멘트 효과와 다릅니다.
이를 사용하는 이유는 비행기의 공력중심을 예측하기위해서 입니다.
주 날갱와 동체를 결합하는 순간 비행기의 공력중심은 변하게 됩니다.
아무래도 그러겠죠?
이를 고려하기 위해서 이를 사용합니다.
$$\frac { d{ { \alpha }_{ local } } }{ d{ { \alpha }_{ W } } } =1\pm \frac { d\varepsilon }{ d{ { \alpha }_{ W } } }$$ |
(154) |
upwash는 +이고 downwash는 -입니다.
위의 식 153에 넣어주면 됩니다.
$$\begin{align} & { { C }_{ M } }=\left( { { C }_{ { { M }_{ { { 0 }_{ F } } } } } }+{ { C }_{ { { M }_{ A{ { C }_{ W } } } } } } \right) +{ { C }_{ { { L }_{ { { \alpha }_{ W } } } } } }\left( \alpha +{ { i }_{ W } }-{ { \alpha }_{ { { 0 }_{ W } } } } \right) \left( \frac { { { X }_{ A{ { C }_{ W\&F } } } }-{ { X }_{ CG } } }{ \overline { { { c }_{ W } } } } \right) \\ & -{ { C }_{ { { L }_{ { { \alpha }_{ H } } } } } }\left( \left( 1-\frac { d\varepsilon }{ d\alpha } \right) \alpha +\frac { d\varepsilon }{ d\alpha } \left( { { \alpha }_{ { { 0 }_{ W } } } }-{ { i }_{ W } } \right) +{ { i }_{ H } }-{ { \alpha }_{ { { 0 }_{ H } } } }+{ { \alpha }_{ \delta } }{ { \delta }_{ E } } \right) \left( \frac { { { X }_{ CG } }-{ { X }_{ A{ { C }_{ H } } } } }{ \overline { { { c }_{ W } } } } \right) \frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ H } } }{ { { S }_{ W } } } \\ & \end{align} \tag{155} \\$$
식 150을 피칭모멘트 계수로 정리하면 식 155이됩니다.
이는 동체의 영향을 포함한 비행기 전체의 피칭모멘트 계수입니다.
$${ { C }_{ { { M }_{ \alpha } } } }={ { C }_{ { { L }_{ { { \alpha }_{ W } } } } } }\left( \frac { { { X }_{ A{ { C }_{ W\&F } } } }-{ { X }_{ CG } } }{ \overline { { { c }_{ W } } } } \right) -{ { C }_{ { { L }_{ { { \alpha }_{ H } } } } } }\left( 1-\frac { d\varepsilon }{ d\alpha } \right) \left( \frac { { { X }_{ CG } }-{ { X }_{ A{ { C }_{ H } } } } }{ \overline { { { c }_{ W } } } } \right) \frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ H } } }{ { { S }_{ W } } } \tag{156} \\$$
식 156는 식 155를 받음각으로 미분한 값입니다.
이를 비행기 받음각 피칭모멘트 효과(Vehicle's angle of attack pitching moment effectiveness)라고 부릅니다.
$${ { C }_{ { { M }_{ \delta E } } } }=-{ { C }_{ { { L }_{ { { \alpha }_{ H } } } } } }{ { \alpha }_{ \delta } }\left( \frac { { { X }_{ CG } }-{ { X }_{ A{ { C }_{ H } } } } }{ \overline { { { c }_{ W } } } } \right) \frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ H } } }{ { { S }_{ W } } } $$ |
(157) |
식 157는 식 155를 엘리베이터 각도로 미분한 값입니다.
이를 비행기의 엘리베이터 피칭모멘트 효과(Elevator pitching moment effectiveness for vehicle)이라 부릅니다.
$${ { C }_{ { { M }_{ { { i }_{ H } } } } } }=-{ { C }_{ { { L }_{ { { \alpha }_{ H } } } } } }\left( \frac { { { X }_{ CG } }-{ { X }_{ A{ { C }_{ H } } } } }{ \overline { { { c }_{ W } } } } \right) \frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ H } } }{ { { S }_{ W } } } $$ |
(158) |
식 158은 식 155를 수평 꼬리날개 붙임각으로 미분한 값입니다.
이를 비행기 꼬리 붙임각 피칭모멘트 효과(Vehicle's tail-incidence pitching moment effectiveness)라고 부릅니다.
$$\begin{align} & { { \left. { { C }_{ M } } \right| }_{ \alpha ={ { \delta }_{ E } }={ { i }_{ H } }=0 } }=\left( { { C }_{ { { M }_{ A{ { C }_{ W } } } } } }+{ { C }_{ { { M }_{ { { 0 }_{ F } } } } } } \right) +{ { C }_{ { { L }_{ { { \alpha }_{ W } } } } } }\left( { { i }_{ W } }-{ { \alpha }_{ { { 0 }_{ W } } } } \right) \left( \frac { { { X }_{ A{ { C }_{ WF } } } }-{ { X }_{ CG } } }{ \overline { { { c }_{ W } } } } \right) \\ & -{ { C }_{ { { L }_{ { { \alpha }_{ H } } } } } }\left( \frac { d\varepsilon }{ d\alpha } \left( { { \alpha }_{ { { 0 }_{ W } } } }-{ { i }_{ W } } \right) -{ { \alpha }_{ { { 0 }_{ H } } } } \right) \left( \frac { { { X }_{ CG } }-{ { X }_{ A{ { C }_{ H } } } } }{ \overline { { { c }_{ W } } } } \right) \left( \frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \right) \left( \frac { { { S }_{ H } } }{ { { S }_{ W } } } \right) \\ & \end{align}$$ |
(159) |
식 159는 식 155에 받음각, 엘리베이터 각도, 꼬리 붙임각 =0을 한 값입니다.
이는 피칭모멘트의 기준이됩니다.
23. NAVION의 피칭모멘트 와 공력중심 예측


Root chord의 앞전 앞부분은 upwash가 작용하고 뒷전 뒷부분은 downwash가 발생합니다.
${ w }_{ { F }_{ i } }$ = i번째 셀의 평균 너비
$\triangle { x }_{ i }$ = 셀 x축길이
${ x }_{ i }$ = i번째 셀까지 길이
17개의 셀로 동체를 칼로 잘랐습니다.
그리고 각 셀마다 중간지점의 세로길이를 너비라 합니다.
원래는 각 점을 합하여 평균을 구해야하지만 일단 대충진행하겠습니다.
각 셀마다 가로길이를 $\triangle { x }_{ i }$이라 합니다.
날개 공력중심에서 셀 중심까지 길이를 구하는 이유는 upwash를 구하기 위해서 사용합니다.
아래 그림을 보시면 알 수 있습니다.

(저기 A는 주날개의 aspect ratio입니다.)
윗 그림을 보시면 x축 0점이 Root chord의 1/4입니다.
upwash는 주 날개 앞부분에서만 작용함으로 동체에 붙은 날개의 앞부분의 셀만 위의 그래프로 계산하고
주 날개 Root chord의 뒷전 이후로는 downwash로 계산해야합니다.
이는 수평꼬리날개 다운워시 받음각을 계산했던 그래프와 동일합니다.
제가 열심히 연필과 자를 이용해서 구해 놓았습니다.
(그림 43 참고)
$$\begin{align} & { { C }_{ { { M }_{ { { \alpha }_{ F } } } } } }\cong \frac { 1 }{ 36.5\times { { S }_{ W } }\times \overline { { { c }_{ W } } } } \sum _{ { { x }_{ i } }=0 }^{ { { x }_{ i } }={ { l }_{ F } } }{ w_{ { { F }_{ i } } }^{ 2 } } \frac { d{ { \alpha }_{ local } } }{ d{ { \alpha }_{ W } } } \left( { { x }_{ i } } \right) \Delta { { x }_{ i } } \\ & =\frac { 1 }{ 36.5\times 184f{ { t }^{ 2 } }\times 5.6715ft } \sum _{ { { x }_{ i } }=0 }^{ { { x }_{ i } }={ { l }_{ F } } }{ w_{ { { F }_{ i } } }^{ 2 } } \frac { d{ { \alpha }_{ local } } }{ d{ { \alpha }_{ W } } } \left( { { x }_{ i } } \right) \Delta { { x }_{ i } } \\ & =\frac { 1 }{ 36.5\times 184f{ { t }^{ 2 } }\times 5.6715ft } \left[ \begin{matrix} { { \left( 3.313 \right) }^{ 2 } }\times 1.25\times 1.327 \\ { { \left( 3.518 \right) }^{ 2 } }\times 1.31\times 1.083 \\ { { \left( 3.812 \right) }^{ 2 } }\times 1.46\times 1.389 \\ { { \left( 4.098 \right) }^{ 2 } }\times 1.76\times 1.699 \\ { { \left( 4.216 \right) }^{ 2 } }\times 0\times 1.814 \\ { { \left( 4.235 \right) }^{ 2 } }\times 0\times 1.295 \\ { { \left( 4.117 \right) }^{ 2 } }\times 0\times 1.695 \\ { { \left( 3.791 \right) }^{ 2 } }\times 0\times 2.35 \\ { { \left( 3.409 \right) }^{ 2 } }\times 0.2\times 1.263 \\ { { \left( 3.057 \right) }^{ 2 } }\times 0.24\times 1.389 \\ { { \left( 2.683 \right) }^{ 2 } }\times 0.31\times 1.612 \\ { { \left( 2.314 \right) }^{ 2 } }\times 0.36\times 1.417 \\ { { \left( 1.928 \right) }^{ 2 } }\times 0.38\times 1.889 \\ { { \left( 1.466 \right) }^{ 2 } }\times 0.41\times 1.556 \\ { { \left( 1.098 \right) }^{ 2 } }\times 0.44\times 1.584 \\ { { \left( 0.668 \right) }^{ 2 } }\times 0.46\times 1.723 \\ { { \left( 0.312 \right) }^{ 2 } }\times 0.48\times 1.633 \\ \end{matrix} \right] \\ & =0.0035\left( /deg \right) \\ & =0.0035\left( /deg \right) \frac { 180\left( deg \right) }{ \pi \left( rad \right) } ={ 0 }{ .2005 }\left( /rad \right) \\ & \end{align}$$ |
(160) |
식 160은 식 153을 정리하여 만든 계수식입니다.
이는 비행기의 공력중심을 예측하기 위해서 계산한 것입니다.
$$\begin{align} & { { X }_{ A{ { C }_{ W\& F } } } }={ { X }_{ A{ { C }_{ W } } } }+\Delta { { X }_{ A{ { C }_{ F } } } } \\ & ={ { X }_{ A{ { C }_{ W } } } }\pm \frac { { { C }_{ { { M }_{ { { \alpha }_{ F } } } } } } }{ { { C }_{ { { L }_{ { { \alpha }_{ W } } } } } } } \overline { { { c }_{ W } } } \\ & =1.8137ft-\frac { 0.2005/rad }{ 4.468/rad } \left( 5.6715ft \right) \\ & ={ 1 }{ .5592 }ft \\ & \end{align}$$ |
(161) |
${ { C }_{ { { M }_{ { { \alpha }_{ F } } } } } }$ 가 양수이면 날개 공력중심에서 빼주고
반대이면 더해줍니다.
위의 공력중심은 동체를 고려한 날개의 공력중심입니다.
여기서 주의해야할 사항은
주익의 양력선 기울기가 마하수에 따라 바뀐다는 것입니다.
이 글에 나오는 거의 모든 계수들은 속도의 함수입니다.
실제 비행기의 계수를 구하려면 속도의 변화에 대해서 일일히 분석해야합니다.
이는 다음 글에서 자세하게 다루겠습니다.
$$\begin{align} & { { C }_{ { { M }_{ { { 0 }_{ F } } } } } }=\frac { \kappa \times { { \alpha }_{ { { 0 }_{ W } } } } }{ 36.5\times { { S }_{ W } }\times \overline { { { c }_{ W } } } \, } \sum _{ { { x }_{ i } }=0 }^{ { { x }_{ i } }={ { l }_{ F } } }{ w_{ { { F }_{ i } } }^{ 2 } } \Delta { { x }_{ i } } \\ & =\frac { 0.87\times \left( -4.95 \right) }{ 36.5\times 184f{ { t }^{ 2 } }\times 5.6715ft } \left[ \begin{matrix} { { \left( 3.313 \right) }^{ 2 } }\times 1.327 \\ { { \left( 3.518 \right) }^{ 2 } }\times 1.083 \\ { { \left( 3.812 \right) }^{ 2 } }\times 1.389 \\ { { \left( 4.098 \right) }^{ 2 } }\times 1.699 \\ { { \left( 4.216 \right) }^{ 2 } }\times 1.814 \\ { { \left( 4.235 \right) }^{ 2 } }\times 1.295 \\ { { \left( 4.117 \right) }^{ 2 } }\times 1.695 \\ { { \left( 3.791 \right) }^{ 2 } }\times 2.35 \\ { { \left( 3.409 \right) }^{ 2 } }\times 1.263 \\ { { \left( 3.057 \right) }^{ 2 } }\times 1.389 \\ { { \left( 2.683 \right) }^{ 2 } }\times 1.612 \\ { { \left( 2.314 \right) }^{ 2 } }\times 1.417 \\ { { \left( 1.928 \right) }^{ 2 } }\times 1.889 \\ { { \left( 1.466 \right) }^{ 2 } }\times 1.556 \\ { { \left( 1.098 \right) }^{ 2 } }\times 1.584 \\ { { \left( 0.668 \right) }^{ 2 } }\times 1.723 \\ { { \left( 0.312 \right) }^{ 2 } }\times 1.633 \\ \end{matrix} \right] \\ & =-0.0288 \\ & \end{align}$$ |
(162) |
식 162는 식 152를 정리하여 계수식으로 만든 것입니다.
(계수만 남기고 넘기면 됨)
이 식에서 유의할 사항은 저번에 구한 0양력 받음각의 부호가 +-둘다 가능하다는 것입니다.
따라서 이 계수도 +-부호가 둘 다 가능합니다.
그리고 $\varkappa $는 아래 그래프를 통해서 구할 수 있습니다.

저는 이 값이 위의 식 162에 나와있듯이 0.87입니다.
$$\begin{align} & { { C }_{ { { M }_{ \alpha } } } }={ { C }_{ { { L }_{ { { \alpha }_{ W } } } } } }\left( \frac { { { X }_{ A{ { C }_{ W\& F } } } }-{ { X }_{ CG } } }{ \overline { { { c }_{ W } } } } \right) -{ { C }_{ { { L }_{ { { \alpha }_{ H } } } } } }\left( 1-\frac { d\varepsilon }{ d\alpha } \right) \left( \frac { { { X }_{ CG } }-{ { X }_{ A{ { C }_{ H } } } } }{ \overline { { { c }_{ W } } } } \right) \frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ H } } }{ { { S }_{ W } } } \\ & =4.468\left( \frac { -1.5592ft-\left( -\left( { { X }_{ L{ { E }_{ MAC } } } }+0.295\overline { { { c }_{ W } } } \right) \right) }{ \overline { { { c }_{ W } } } } \right) -3.9524\left( 1-0.56 \right) \left( \frac { -\left( { { X }_{ L{ { E }_{ MAC } } } }+0.295\overline { { { c }_{ W } } } \right) -\left( -\left( 15.712+1.1501 \right) \right) }{ \overline { { { c }_{ W } } } } \right) \left( 0.9 \right) \left( \frac { 43 }{ 184 } \right) \\ & =4.468\left( \frac { -1.5592+\left( 0.3958+0.295\times 5.6715 \right) }{ 5.6715 } \right) -3.9524\left( 1-0.56 \right) \left( \frac { -\left( 0.3958+0.295\times 5.6715 \right) +\left( 15.712+1.1501 \right) }{ 5.6715 } \right) \left( 0.9 \right) \left( \frac { 43 }{ 184 } \right) \\ & =-{ 0 }{ .5525 }\left( /rad \right) \\ & \end{align} \tag{163} \\$$
식 163 비행기의 받음각 피칭모멘트 효과(Vehicle's angle of attack pitching moment effectiveness)
이 계수는 비행기 설계에 매우 중요한 개념입니다.
트림조건을 찾을때 자세히 말씀드리겠습니다.
$$\begin{align} & { { C }_{ { { M }_{ \delta E } } } }=-{ { C }_{ { { L }_{ { { \alpha }_{ H } } } } } }{ { \alpha }_{ \delta } }\left( \frac { { { X }_{ CG } }-{ { X }_{ A{ { C }_{ H } } } } }{ \overline { { { c }_{ W } } } } \right) \frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ H } } }{ { { S }_{ W } } } \\ & =-3.9524\left( 1.1349 \right) \left( \frac { -\left( 0.3958+0.295\times 5.6715 \right) +\left( 15.712+1.1501 \right) }{ 5.6715 } \right) \left( 0.9 \right) \left( \frac { 43 }{ 184 } \right) \\ & =-{ 2 }{ .4608 }\left( { /rad } \right) \\ & \end{align} \tag{164} \\$$
식 164: 비행기의 엘리베이터 피칭모멘트 효과(Elevator pitching moment effectiveness for vehicle)
$$\begin{align} & { { C }_{ { { M }_{ { { i }_{ H } } } } } }=-{ { C }_{ { { L }_{ { { \alpha }_{ H } } } } } }\left( \frac { { { X }_{ CG } }-{ { X }_{ A{ { C }_{ H } } } } }{ \overline { { { c }_{ W } } } } \right) \frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ H } } }{ { { S }_{ W } } } \\ & =-3.9524\times \left( \frac { -\left( 0.3958+0.295\times 5.6715 \right) +\left( 15.712+1.1501 \right) }{ 5.6715 } \right) \left( 0.9 \right) \left( \frac { 43 }{ 184 } \right) \\ & =-{ 2 }{ .1683 }\left( { /rad } \right) \\ & \end{align} \tag{165} \\$$
식 165: 비행기 꼬리 붙임각 피칭모멘트 효과(Vehicle's tail-incidence pitching moment effectiveness)
$$\begin{align} & { { \left. { { C }_{ M } } \right| }_{ \alpha ={ { \delta }_{ E } }={ { i }_{ H } }=0 } }=\left( { { C }_{ { { M }_{ A{ { C }_{ W } } } } } }+{ { C }_{ { { M }_{ { { 0 }_{ F } } } } } } \right) +{ { C }_{ { { L }_{ { { \alpha }_{ W } } } } } }\left( { { i }_{ W } }-{ { \alpha }_{ { { 0 }_{ W } } } } \right) \left( \frac { { { X }_{ A{ { C }_{ W\& F } } } }-{ { X }_{ CG } } }{ \overline { { { c }_{ W } } } } \right) \\ & -{ { C }_{ { { L }_{ { { \alpha }_{ H } } } } } }\left( \frac { d\varepsilon }{ d\alpha } \left( { { \alpha }_{ { { 0 }_{ W } } } }-{ { i }_{ W } } \right) -{ { \alpha }_{ { { 0 }_{ H } } } } \right) \left( \frac { { { X }_{ CG } }-{ { X }_{ A{ { C }_{ H } } } } }{ \overline { { { c }_{ W } } } } \right) \left( \frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \right) \left( \frac { { { S }_{ H } } }{ { { S }_{ W } } } \right) \\ & =\left( -0.0908-0.0288 \right) +4.468\left( /rad \right) \left( \frac { \pi \left( rad \right) }{ 180\left( deg \right) } \right) \left( 0-\left( -4.95 \right) \right) \left( \frac { -1.5592+\left( 0.3958+0.295\times 5.6715 \right) }{ 5.6715 } \right) \\ & -3.9524\left( /rad \right) \left( \frac { \pi \left( rad \right) }{ 180\left( deg \right) } \right) \left( 0.56\left( -4.95-2 \right) -0.9997 \right) \left( \frac { -\left( 0.3958+0.295\times 5.6715 \right) +\left( 15.712+1.1501 \right) }{ 5.6715 } \right) \left( 0.9 \right) \left( \frac { 43 }{ 184 } \right) \\ & =0.1142 \\ & \end{align} \tag{166} \\$$
이 값은 전통적으로 +값이나옵니다.
$${ { \overline { X } }_{ A{ { C }_{ vehicle } } } }\triangleq \frac { { { X }_{ A{ { C }_{ Vehicle } } } } }{ { { \overline { c } }_{ W } } } =\frac { { { C }_{ { { L }_{ { { \alpha }_{ W } } } } } }\left( \frac { { { X }_{ A{ { C }_{ W\& F } } } } }{ { { \overline { c } }_{ W } } } \right) +{ { C }_{ { { L }_{ { { \alpha }_{ H } } } } } }\left( 1-\frac { d\varepsilon }{ d\alpha } \right) \left( \frac { { { X }_{ A{ { C }_{ H } } } } }{ { { \overline { c } }_{ W } } } \right) \frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ H } } }{ { { S }_{ W } } } }{ { { C }_{ { { L }_{ { { \alpha }_{ W } } } } } }+{ { C }_{ { { L }_{ { { \alpha }_{ H } } } } } }\left( 1-\frac { d\varepsilon }{ d\alpha } \right) \frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ H } } }{ { { S }_{ W } } } } \tag{167} \\$$
식 167은 비행기의 공력 중심 위치(Location for the vehicle's aerodynamic center)입니다.
이 식은 비행기의 피칭모멘트 받음각 효과인 식 163에 계수를 0으로 두고 Xcg를 좌변으로
나머지 수식을 우변으로 옮겨서 만들었고 Xcg의 이름을 저렇게 바꾼것입니다.
원래 Xcg에는 Xref라는 이름으로 들어있습니다.
하지만 비행기의 계수를 구할때는 모두 Xcg로 계산합니다.
이를 공력 중심의 정의에 의해서 만들어진 것입니다.
공력 중심의 정의가 바로 받음각에 따라 피칭모멘트가 변하지 않는 지점이니까요.
따라서 식 163이 얼마나 중요한 수식일지 감이 오시리라 생각합니다.
(제가 많이 부족해서 설명이 참... ㅠㅠ 죄송한 마음입니다.)
비행기의 공력중심이 주 날개의 공력중심과 같다고 생각하셨나요?
아닙니다.. 저도 그렇게 생각했습니다.
정진센터의 순기능이 이런게 아닐까합니다.
아직 많이 깊게 공부하지 않은 분들에게 지래짐작을 하지 않도록 하는 것이죠.
물론 저도 그렇게 많이 알지는 못하지만 이런 부분을 쓸때는 보람을 느낍니다.
쓸모가 있다고 느껴지는 부분입니다. ㅋ
$$\begin{align} & { { { \bar { X } } }_{ A{ { C }_{ vehicle } } } }\triangleq \frac { { { X }_{ A{ { C }_{ Vehicle } } } } }{ { { { \bar { c } } }_{ W } } } =\frac { { { C }_{ { { L }_{ { { \alpha }_{ W } } } } } }\left( \frac { { { X }_{ A{ { C }_{ W\& F } } } } }{ { { { \bar { c } } }_{ W } } } \right) +{ { C }_{ { { L }_{ { { \alpha }_{ H } } } } } }\left( 1-\frac { d\varepsilon }{ d\alpha } \right) \left( \frac { { { X }_{ A{ { C }_{ H } } } } }{ { { { \bar { c } } }_{ W } } } \right) \frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ H } } }{ { { S }_{ W } } } }{ { { C }_{ { { L }_{ { { \alpha }_{ W } } } } } }+{ { C }_{ { { L }_{ { { \alpha }_{ H } } } } } }\left( 1-\frac { d\varepsilon }{ d\alpha } \right) \frac { { { q }_{ H } } }{ { { q }_{ \infty } } } \frac { { { S }_{ H } } }{ { { S }_{ W } } } } \\ & =\frac { 4.468\left( \frac { -1.5592 }{ 5.6715 } \right) +3.9524\left( 1-0.56 \right) \left( \frac { -{ 16 }{ .8621 } }{ 5.6715 } \right) }{ 4.468+3.9524\left( 1-0.56 \right) \left( 0.9 \right) \left( \frac { 43 }{ 184 } \right) } \\ & =-{ 0 }{ .479 } \\ & \\ & \therefore { { X }_{ A{ { C }_{ Vehicle } } } }={ { { \bar { X } } }_{ A{ { C }_{ vehicle } } } }\times \overline { { { c }_{ W } } } \\ & =-0.479\times 5.6715ft \\ & =-2.717ft \\ & \end{align} \tag{167} \\$$
식 168은 비행기 공력중심의 위치를 계산한 결과입니다.
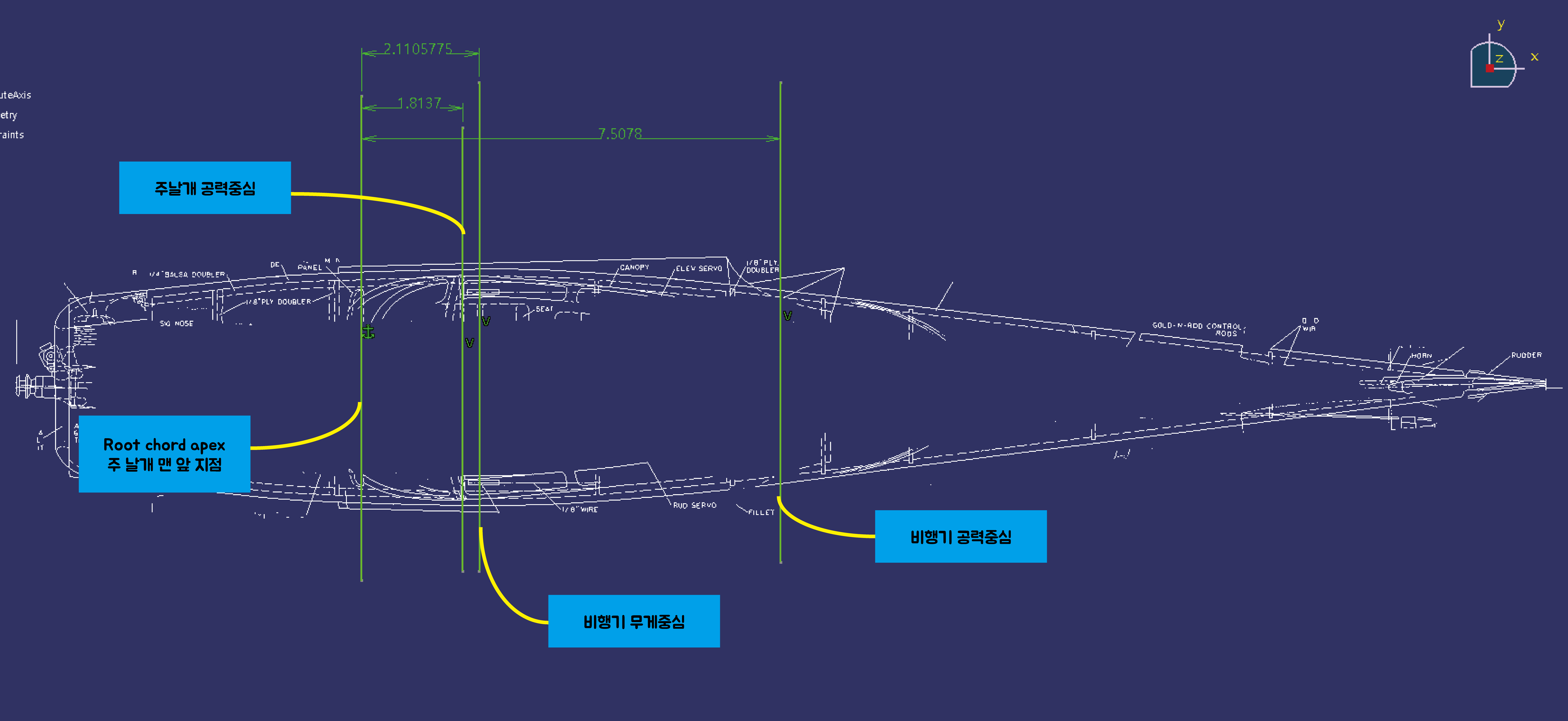
실제 계산결과 비행기의 공력중심은 주 날개의 공력중심보다 훨씬 뒤에 위치하는 것을 확인했습니다.
놀랍습니다.
이번 글에서는 비행기의 공기력을 어떻게 표현하는 지와 비행기의 피칭모멘트에 대해서 알아봤습니다.
다음 글에서는 비행기의 트림조건(Trim condition)에 대해서 알아보겠습니다.
'비행기 설계' 카테고리의 다른 글
| [프로젝트1-30] openvsp를 이용한 CDF구하기 (0) | 2021.06.20 |
|---|---|
| [프로젝트1-29] 비행기의 트림조건 찾기 (0) | 2020.08.29 |
| [프로젝트1-27] 지금까지 구한 계수들 정리 (0) | 2020.08.20 |
| [프로젝트1-26] 3차원 꼬리날개 분석2 (0) | 2020.08.14 |
| [프로젝트1-25] 3차원 꼬리날개 분석 (0) | 2020.08.09 |
