티스토리 뷰

NAVION 공력 특성에 대한 조종면의 영향들
NAVION 1,2,3차 보고서에서는
비행기의 날개에만 초점을 맞춰서 선형화에 필요한 각종 계수들과
함수들에 대해서 말씀드렸습니다.
이번 4차 보고서에서는 비행기의 Flap, aileron, elevator, rudder와 같은
조종면들에 대한 계수들과 함수들에 대해서 말씀드리겠습니다.

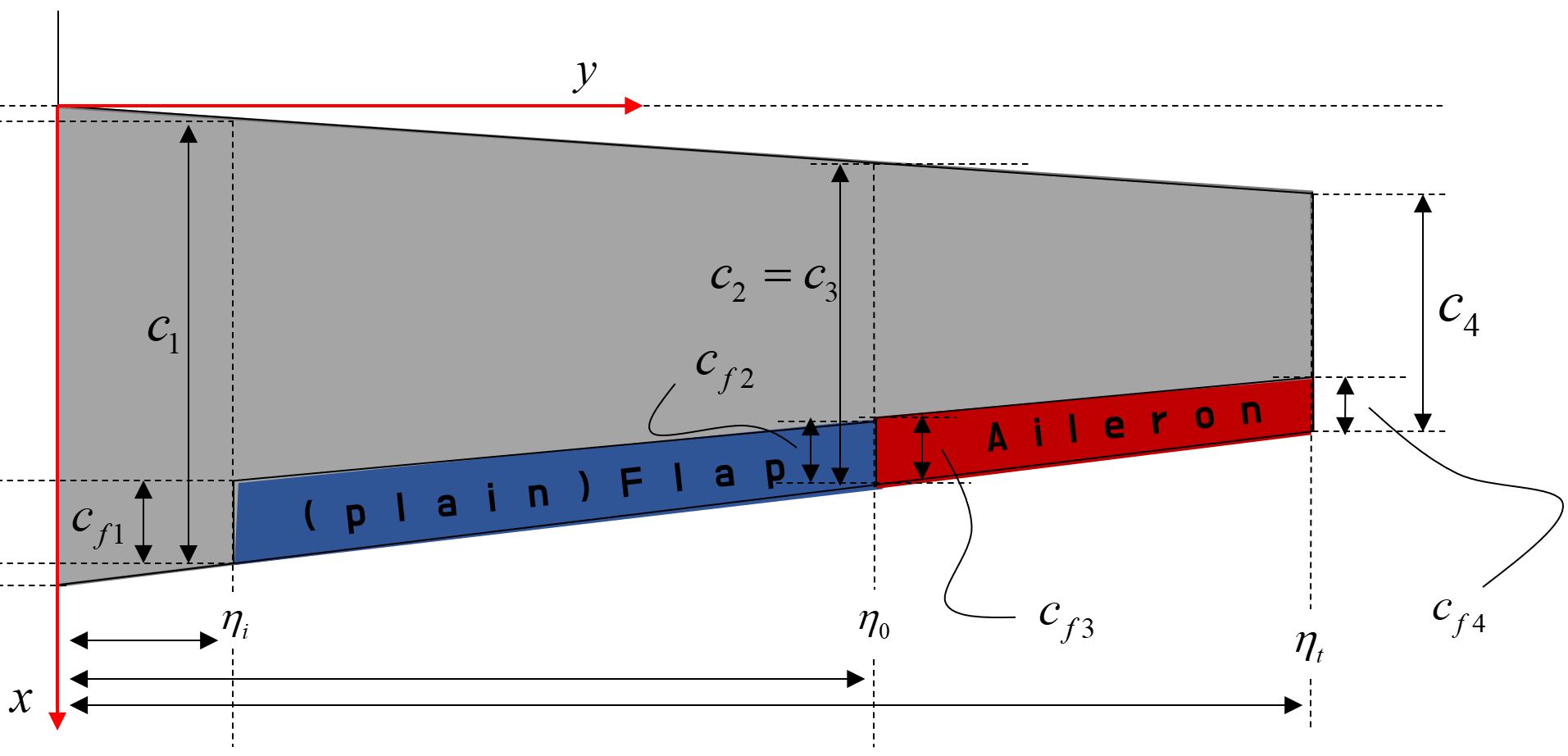
표. 5 그림 7의 값들
$\frac{{{c}_{f}}}{c}$는 각각의 조종면에서 상수 |
|
${{\eta }_{i}}$ |
3.92 ft |
${{\eta }_{o}}$ |
11.314 ft |
${{\eta }_{t}}$ |
16.173 ft |
\[\frac{{{c}_{f1}}}{{{c}_{1}}}=\frac { { { c }_{ f2 } } }{ { { c }_{ 2 } } } \] |
0.2 |
\[\frac{{{c}_{f3}}}{{{c}_{3}}}=\frac { { { c }_{ f4 } } }{ { { c }_{ 4 } } } \] |
0.25 |
${ c }_{ 1 }$ |
6.382 ft |
${ c }_{ 2 }={ c }_{ 3 }$ |
4.924 ft |
${ c }_{ 4 }$ |
3.967 ft |
${ c }_{ f1 }$ |
1.276 ft |
${ c }_{ f2 }$ |
0.985 ft |
${ c }_{ f3 }$ |
1.109 ft |
${ c }_{ f4 }$ |
0.873 ft |
위의 값들을 구하기 위해서 고생 좀 했습니다.

그림 9를 보시면 플랩의 면적과 에일러론의 면적의 차이를 보실 수 있습니다.
전체 날개의 면적이 184인데 플랩이 83.6을 차지합니다.
그리고 에일러론의 면적은 바로 5.4로 내려갔습니다.
처음에는 천하의 NASA가 실수를 했나?
라고 생각했으나..
플랩의 면적은 단순히 플랩 자체만의 면적이 아닌 플랩이 위치해 있는
날개 전체의 면적입니다.
그리고 83.6이라는 값은 양쪽 플랩의 면적을 합한 값입니다.
왜 굳이 이렇게 표현했는지는 모르겠으나..
Modern flight dynamic책을 보면 얼추 이해는 갑니다.

그림 10을 보시면 ${{\eta }_{i}}$에서 ${{\eta }_{o}}$까지가
플랩이 위치해있는 위치이며 그 플랩만의 면적을 계산하는 것이 아니라
그 앞에 해당하는 날개 전체의 면적을 플랩의 면적으로 보고 있습니다.
물론 이 글에서 나올 식들을 보시면 적분을 통해 날개 전체의 면적을 이용하고는 있습니다만...
NASA에서 저렇게 표기해 놓아서 조금 혼동이 됐었습니다.
게다가 에일러론은 그냥 에일러론 자체만의 면적만 적어두었습니다.
그래도 최대한 실제 NAVION과 부합하도록 조종면의 사이즈를 맞추었습니다.
11. 플랩 양력 효과 (Flap lift effectiveness), ${ { C }_{ { { L }_{ \delta F } } } }$ 와 Alternate flap effectiveness parameter, ${{\alpha }_{\delta }}$ 구하기
Alternate flap effectiveness parameter,${{\alpha }_{\delta }}$를 뭐라 번역해야 할지 모르겠습니다. ㅠㅠ
대체 플랩 효과 계수? 어쨌든 플랩을 정의하는 하나의 계수입니다.
$${ { C }_{ { { L }_{ \delta F } } } }=\frac { 2 }{ S } \int _{ { { \eta }_{ i } } }^{ { { \eta }_{ o } } }{ { { C }_{ { { l }_{ \delta } } } }\left( y \right) c\left( y \right) dy }$$ |
(50) |
식 50은 3차원 날개의 플랩 양력 효과를 구할 수 있는 함수입니다.
c(y)는 저번에 구해서 알지만 모르는 함수가 포함되어있습니다.
그건 식 51로 구할 수 있습니다.
이는 2차원 날개의 플랩 양력 효과를 의미하며 적분하여 3차원 날개를 구하기 위함입니다.
$${ { C }_{ { { l }_{ \delta } } } }=\frac { 1 }{ \beta } \left( \frac { { { C }_{ { { l }_{ \delta } } } } }{ { { \left. { { C }_{ { { l }_{ \delta } } } } \right| }_{ theory } } } \right) { { \left. { { C }_{ { { l }_{ \delta } } } } \right| }_{ theory } }\left( /rad \right) $$ |
(51) |
식 51의 $\beta$는 저번에도 한번 풀었습니다.
프란델의 아음속 압축성 계수입니다.
식 52로 구하시면 됩니다.
그리고 괄호 안에 있는 분수 값과 괄호 밖에 있는 값을 구해야 합니다.
이 값은 그림 11, 12를 통해서 구할 수 있습니다.
$$\beta =\sqrt { \left( 1-M_{ \infty }^{ 2 } \right) }$$ |
(52) |
식 52는 Prandtl-Glauert subsonic compressibility factor입니다.

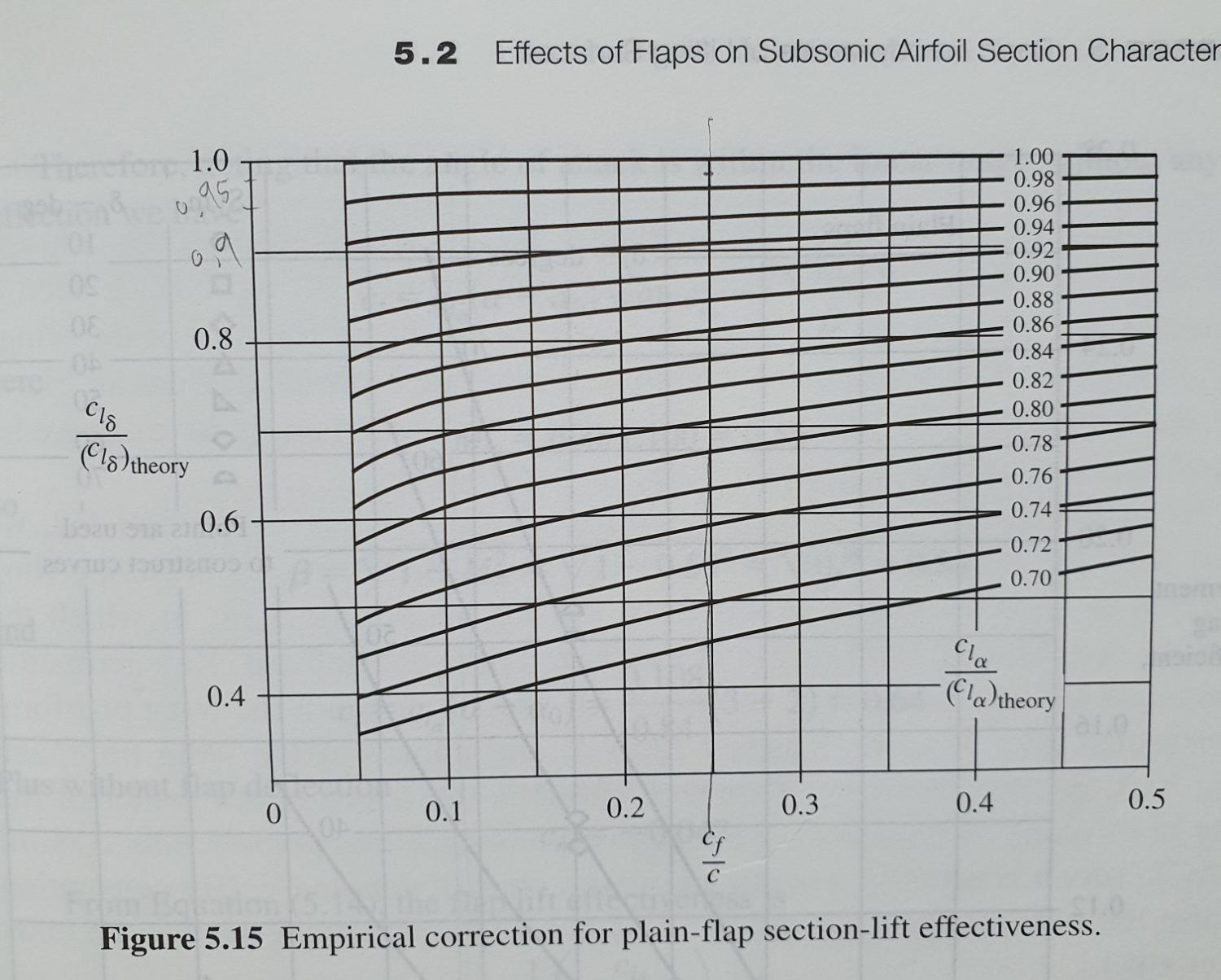
그림 11의 이해를 돕기 위해서 간략히 첨언하도록 하겠습니다.
제가 보고서 1차 초기에 날개에는 NACA4415 에어포일만 사용한다고 한 것을 기억하시나요?
NACA 4자리는 마지막 두 숫자가 t/c를 의미합니다.
따라서 NAVION은 0.15입니다.
그리고 cf/c는 에일러론과 (플레인 플랩)이 서로 다릅니다.
에일러론은 0.25이고 (플레인 플랩)은 0.2입니다.
따라서 에일러론의 ${{C}_{{{l}_{\delta }}}}\left( theory \right)$값은 약 4.25(/rad)이고
플레인 플랩의 값은 약 3.75(/rad)입니다.
참고로 CFD 없이 손으로 조종면을 설계 및 해석을 하려면 cf/c값이 같아야 합니다.
예를 들어 위에서 에일러론은 0.25라 하였고 플랩은 0.2라고 한 것처럼
조종면 안에서는 일정한 cf/c값을 가져야 합니다.
(이해되시나요? 쉽게 말하는 법을 모르겠습니다 ㅠㅠ 으아아아아)
$$\frac{{{C}_{{{l}_{\delta }}}}}{{{C}_{{{l}_{\delta }}}}\left( theory \right)}$$ |
(53) |
$$\frac{{{C}_{{{l}_{\alpha }}}}}{{{C}_{{{l}_{\alpha }}}}\left( theory \right)}$$ |
(54) |
그림 12를 보고 식 53 값을 구하려면 식 54의 값을 알고 있어야 합니다.
$$\frac { { { C }_{ { { l }_{ \alpha } } } } }{ { { C }_{ { { l }_{ \alpha } } } }\left( theory \right) } =\frac { 0.105/{ deg } }{ 2\pi (/{ rad }) } \times \frac { 180{ (deg) } }{ \pi { (rad) } } ={ 0 }{ .9575 }$$ |
(55) |
식 54를 푼 것입니다. 단위에 주의하세요!
$$\frac { { { C }_{ { { l }_{ \delta } } } } }{ { { C }_{ { { l }_{ \delta } } } }\left( theory \right) } (Aileron) = 0.93$$ |
(56) |
식 56은 에일러론에 해당하는 값으로
그림 12를 보고 찾았습니다.
$$\frac { { { C }_{ { { l }_{ \delta } } } } }{ { { C }_{ { { l }_{ \delta } } } }\left( theory \right) } (plain flap) = 0.92$$ |
(57) |
식 55 값은 에일러론과 플랩의 공통적인 계수이고
식 56과 57은 각각 해당하는 계수입니다.
이제 ${{C}_{{{l}_{\delta }}}}$를 구해봅시다.

사실 아래 식 58과 59를 구하기 위해서 위의 복잡한 과정을 거쳤습니다.
$$\begin{align} & { { C }_{ { { l }_{ \delta } } } }\left( Aileron \right) =\frac { 1 }{ \beta } \left( \frac { { { C }_{ { { l }_{ \delta } } } } }{ { { \left. { { C }_{ { { l }_{ \delta } } } } \right| }_{ theory } } } \right) { { \left. { { C }_{ { { l }_{ \delta } } } } \right| }_{ theory } } \\ & =\frac { 1 }{ 0.98 } \left( 0.93 \right) \left( 4.25/rad \right) \\ & ={ 4 }{ .0332( }/rad)=0.0704\left( /deg \right) \\ & \end{align}$$ |
(58) |
$$\begin{align} & { { C }_{ { { l }_{ \delta } } } }\left( Plain flap \right) =\frac { 1 }{ \beta } \left( \frac { { { C }_{ { { l }_{ \delta } } } } }{ { { \left. { { C }_{ { { l }_{ \delta } } } } \right| }_{ theory } } } \right) { { \left. { { C }_{ { { l }_{ \delta } } } } \right| }_{ theory } } \\ & =\frac { 1 }{ 0.98 } \left( 0.92 \right) \left( 3.75/rad \right) \\ & ={ 3 }{ .5204( }/rad)=0.0614\left( /deg \right) \\ & \end{align}$$ |
(59) |
식 58과 59는 3차원 값을 구하기 위한
2차원의 날개에 대한 플랩 양력 효과였습니다.
그럼 이제 ${{C}_{{{L}_{\delta }}}}$값을 구해봅시다.
(에일러론은 식이 달라서 다음에...
식 58을 사용해서 구함
$$\begin{align} & { { C }_{ { { L }_{ \delta F } } } }(Plain flap)=\frac { 2 }{ S } \int _{ { { \eta }_{ i } } }^{ { { \eta }_{ o } } }{ { { C }_{ { { l }_{ \delta } } } }\left( y \right) c\left( y \right) dy } \\ & =\frac { 2 }{ 184f{ { t }^{ 2 } } } \int _{ 3.92ft }^{ 11.314ft }{ 3.5204\left( /rad \right) \left( 7.1545-0.1971y \right) }dy \\ & =1.5995\left( /rad \right) \\ & \end{align}$$ |
(60) |
이렇게 3차원 날개에 대한 플랩 양력 효과는 식 60으로 나왔습니다.
당연히 식 50을 사용해서 만들었습니다.
적분할 때 $\eta$값에 주의해야 합니다.
어떠신가요?
너무 복잡하죠?
사실 비행기는 복잡합니다.
하지만 우리 이렇게 생각해봅시다.
1. 비행기를 알려면 기준이 필요하다.
2. 그 기준을 양력 효과니 상반각 효과니 해서 표현한다.
3. 각 값들을 이용해서 시뮬레이션하여 움직임을 예측할 수 있다.
4. 다른 비행기도 1~3과정을 반복해서 비교하자.
5. 원하는 특성을 가진 비행기를 만들자.
위와 같은 방법으로 우리는 어두운 암흑 속에서
비행기란 무엇인지..
그 시야를 넓힐 수 있습니다.
만약 저 식들이 어떻게 나왔는지 알고 싶으신 분들은
Schmidt, Modern flight dynamics 책을 천천히 공부하시는 것을 추천합니다.
제가 2년 동안 각각의 식들을 증명하고 일일이 풀었습니다.
그것까지 하기에는 우리의 갈길이 멉니다.
여러분들은 빠르게 따라오시기 바랍니다.
수식을 풀 수만 있으면 됩니다.
저기 나오는 수식을 푸는 것은 일반 고등학교만
나왔어도 할 수 있습니다.
(파이팅!)
$${{\alpha }_{\delta }}\triangleq \frac{{{C}_{{{L}_{\delta }}}}}{{{C}_{{{L}_{\alpha }}}}}$$ |
(61) |
식 61는 Alternate flap effectiveness parameter입니다.
수식을 보시면 아시겠지만 위에서 구한 플랩 양력 효과와
날개 양력선 기울기의 비율임을 알 수 있습니다.
(그냥 그런가 보다 ~)
$${ { \alpha }_{ \delta } }\left( Flap \right) \triangleq \frac { { { C }_{ { { L }_{ \delta F } } } } }{ { { C }_{ { { L }_{ \alpha } } } } } =\frac { 1.5995/rad }{ 4.42/rad } =0.3619$$ |
(62) |
식 62는 플랩의 Alternate flap effectiveness parameter입니다.
역시 플랩 값이 더 큰 것을 알 수 있습니다.
긴 글 읽어주셔서 감사합니다.
내용을 명확하게 말해주지도 못하고
수식만 가득하여 죄송한 마음입니다.
하지만 이 수식들은 RC 비행기 설계에 피가 되고 살이 되는
중요한 수식들이니
이 글을 읽으시면서 가볍게 아 이런 게 있구나! 하며
읽어주시면 좋겠습니다.
이상 정진센터였습니다.

그럼 이만~
'비행기 설계' 카테고리의 다른 글
| [프로젝트1-25] 3차원 꼬리날개 분석 (0) | 2020.08.09 |
|---|---|
| [프로젝트1-24] 주익 조종면 해석 2 (0) | 2020.08.04 |
| [프로젝트1-22] 3차원 날개 해석 3 (2) | 2020.07.28 |
| [프로젝트1-21] 3차원 날개 해석 2 (2) | 2020.07.24 |
| [프로젝트1-20] 3차원 날개 해석 (0) | 2020.07.23 |
